Bounds on the OR-rank of Kronecker products

Real rank is multiplicative under Kronecker product

Boolean rank is not multiplicative under Kronecker product

A rank-$1$ matrix $A$ consists of one all-$1$ submatrix (a rectangle), and has $0$s elsewhere. The OR-rank (known also as Boolean rank or cover number) of a Boolean matrix $A$, denoted by $\rk{A}$, is the minimum number $r$ of rank-$1$ matrices $A_1,\ldots,A_r$ such that $A$ can be written as the componentwise OR $A=\bigvee_{t=1}^r A_t$ of these matrices [in the book, we denoted this rank as $\br{A}$]. That is, we have $A[i,j]=\bigvee_{t=1}^r A_t[i,j]$ for every position $(i,j)$. In terms of rectangles (instead of rank-$1$ matrices), an equivalent definition of $\rk{A}$ is as follows. A cover of a matrix $A$ is a collection $\R$ of rectangles in $A$ such that every $1$-entry of $A$ belongs to at least one of these rectangles. Then $\rk{A}$ is the minimum number of rectangles in a cover of $A$. It is easy to verify that \[ \rk{A\otimes B}\leq \rk{A}\cdot\rk{B}\,. \] However, unlike for the real rank, the converse inequality $\rk{A\otimes B}\geq \rk{B}\cdot\rk{B}$ does not need to hold. For example, let $C_n=J_n-I_n$ be the $n\times n$ matrix with $0$s on the diagonal and $1$s elsewhere else $(J_n$ is the all-$1$ matrix, and $I_n$ is the identity matrix).

It is easy to show that $\rk{C_n}\leq 2\log(2n)$: label the rows and columns by binary vectors of length $m=\lceil \log n\rceil\leq \log(2n)$ and for every $l=1,\ldots,m$ consider the rectangle $R_{i,\sigma}$ such that the labels of rows of $R_i$ have the same value $\sigma\in\{0,1\}$ in the $i$th position, while the labels of columns of $R_i$ have the opposite value $1-\sigma$ in that position. In fact, De Caen, Gregory, and Pullman [3] have show that an asymptotically tight bound $\rk{C_n}=(1+o(1))\log n$; in particular, $\rk{C_n}\geq \log n$.

On the other hand, Lemma 2 (below) directly yields an upper bound¹ $\rk{C_n\otimes C_n}=O(\log n)$ for all sufficiently large $n$; thus, $\rk{C_n\otimes C_n}\ll \rk{C_n}^2$.

A lower bound

Lemma 1 (Haviv and Parnas [4]): For any two Boolean matrices $A$ and $B$, we have \[ \rk{A\otimes B}\geq \frac{|A|}{s(A)}\cdot \rk{B}\,. \]

Proof: The matrix $A\otimes B$ is obtained from the matrix $A$ by replacing every it $1$-entry by the matrix $B$ (we will refer to such submatrices of $A\otimes B$ as $B$-submatrices), and replacing every $0$-entry of $A$ by the all-$0$ matrix of the same dimension as $B$. Let $\R$ be a cover of $A\otimes B$ with $|\R|=\rk{A\otimes B}$ rectangles. A sub-rectangle of $A\otimes B$ induced by a rectangle $R\in\R$ is the restriction of $R$ onto some $B$-submatrix of $A\otimes B$. Let $\ell(R)$ denote the number of sub-rectangles induced by a rectangle $R$, and use double-counting to estimate the sum \[ \ell(\R)=\sum_{R\in\R}\ell(R)\,. \] Since each rectangle $R\in\R$ induces at most one sub-rectangle in each $B$-submatrix of $A\otimes B$, we have $\ell(R) \leq s(A)$ for every rectangle $R\in\R$. This gives an upper bound \[ \ell(\R)\leq |\R|\cdot s(A)\,. \] On the other hand, for every $B$-submatrix of $A\otimes B$, the sub-rectangles induced by the rectangles of $\R$ must cover the matrix $B$. So, altogether, the rectangles in the covering $\R$ must induce at least $\rk{B}$ subrectangles in each $B$-submatrix. Since the matrix $A\otimes B$ has $|A|$ $B$-submatrices, this gives a lower bound \[ \ell(\R)\geq |A|\cdot \rk{B}\,, \] and the desired lower bound $\rk{A\otimes B}=|\R|\geq \rk{B}\cdot|A|/s(A)$ on the number of rectangles follows. $\Box$

Upper bound for Kronecker products of dense matrices

Using an appropriate modification of a probabilistic argument used by Alon [1], I have proved in [5] that $\rk{A}=O(k\ln n)$ holds for any Boolean $k$-dense $n\times n$ matrix $A$. Actually, a similar argument yields a similar upper bound also for Kronecker products of dense matrices.

Lemma 2: Let $A$ and $B$ be Boolean $n\times n$ matrices, and $a,b\geq 1$. If $A$ is $a$-dense and $B$ is $b$-dense, then $\rk{A\otimes B}=O(ab\ln n)$.

Proof: We may assume without loss of generality² that every column of $A$ has at most $a$ zeros, and every column of $b$ has at most $b$ zeros. Let $R_A$ (resp., $R_B$) be the set of all indices of rows of the matrix $A$ (resp., of the matrix $B$), and let $C_A$ (resp., $C_B$) be the set of all indices of columns of the matrix $A$ (resp., of the matrix $B$). For a column $j\in C_A$ of $A$, let $Z_A(j)=\{i\in R_A\colon A[i,j]=0\}$ be the set of $|Z_A(j)|\leq a$ rows of $A$ with a $0$ in the $j$th column. Similarly, for column $j\in C_B$ of $B$, let $Z_B(j)=\{i\in R_B\colon B[i,j]=0\}$ be the set of $|Z_A(j)|\leq b$ rows of $B$ with a $0$ in the $j$th column.

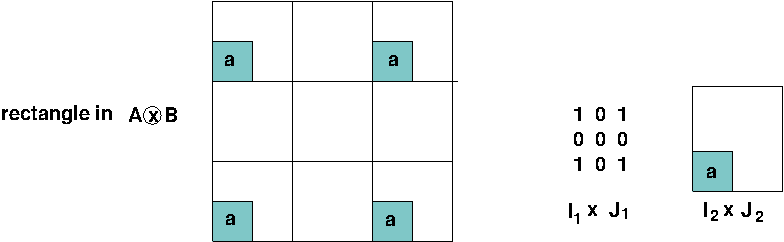
We will use a probabilistic argument to cover the $1$s of the matrix $A\otimes B$ by rectangles of a very special form $I_1\times J_1\times I_2\times J_2$, where $I_1\subseteq R_A$, $J_1\subseteq C_A$, $I_2\subseteq R_B$, and $J_2\subseteq C_B$. That is, we take some rectangle $I_1\times J_1$ in the matrix $A$, and replace each its $1$-entry by one and the same rank-$1$ matrix $M\leq B$ corresponding to the rectangle $I_2\times J_2$ in $B$. Here is an illustration:

So, consider the following probabilistic procedure of choosing a rectangle $\I_1\times \J_1\times \I_2\times \J_2$ in $A\otimes B$.

1. Pick every row $i\in R_A$ of $A$ independently, with probability $p=1/(a+1)$ to get a subset $\I_1\subseteq R_A$ of rows of $A$.
2. Pick every row $i\in R_B$ of $B$ independently, with probability $q=1/(b+1)$ to get a subset $\I_2\subseteq R_B$ of rows of $B$.
3. Set $\J_1:=\{j\in C_A\colon \mbox{$A[i,j]=1$ for all $i\in\I_1$}\}$.
4. Set $\J_2:=\{j\in C_B\colon \mbox{$B[i,j]=1$ for all $i\in\I_2$}\}$.

Fix an arbitrary entry $(i_A,j_A,i_B,j_B)$ of the matrix $A\otimes B$. The corresponding entry of $A\otimes B$ is $A\otimes B[i_A,j_A,i_B,j_B]=A[i_A,j_A]\cdot B[i_B,j_B]$. Let $\alpha$ be the probability that this entry belongs to the random rectangle $\I_1\times \J_1\times \I_2\times \J_2$. The entry $(i_A,j_A,i_B,j_B)$ belongs to this rectangle if the following event happens: \[ i_A\in\I_1\ \mbox{ and }\ Z_A(j_A)\cap \J_1=\emptyset \ \mbox{ and }\ i_B\in\I_2\ \mbox{ and }\ Z_B(j_B)\cap \J_2=\emptyset\,. \] Since $|Z_A(j_A)|\leq a$ and $|Z_B(j_B)|\leq b$, we have a lower bound: \[ \alpha\geq p(1-p)^aq(1-q)^b=p(1-\tfrac{1}{a+1})^a q(1-\tfrac{1}{b+1})^b\geq pq/e^2\,, \] where the second inequality holds because $1-1/(a+1)\geq e^{-1/a}$ and $1-1/(b+1)\geq e^{-1/b}$. Apply this procedure $t$ times to get $t$ random rectangles in the matrix $A\otimes B$. Since this matrix has $|A\otimes B|\leq n^4$ $1$-entries, the probability that some of these entries belongs to none of the $t$ picked rectangles is at most \[ |A\otimes B|(1-\alpha)^t\leq n^4(1-pq/e^2)^t\leq n^4e^{-tpq/e^2}=\exp(4\ln n - t/[e^2(a+1)(b+1)])\,, \] which is $<1$ for $t > 8e^2ab\ln n$. $\Box$

Structural upper bounds

Lemma 3 ([4]): Let $A$ and $B$ be Boolean matrices. If $A_1,\ldots,A_r$ and $B_1,\ldots,B_r$ are sequences of matrices forming an $r$-cover of the pair $(A,B)$, then $A\otimes B=\bigvee_{t=1}^r A_t\otimes B_t$ and, hence, $\rk{A\otimes B}\leq \sum_{t=1}^r \rk{A_t\otimes B_t}$.

Proof: The matrix $A\otimes B$ can be viewed as a matrix of blocks, where the block of $A\otimes B$ corresponding to the $(i,j)$ entry of matrix $A$ is $A[i,j]\cdot B$. To prove the equality of the two matrices $A\otimes B$ and $\bigvee_{t=1}^r A_t\otimes B_t$, it suffices to compare the matrices block by block. So consider an arbitrary block indexed by $(i,j)$. Suppose first that $A[i,j] = 0$. In this case, the $(i,j)$th block of $A\otimes B$ is the zero matrix. Since $A=\bigvee_{t=1}^r A_t$, we have $A_t[i,j]=0$ for all $t=1,\ldots,r$. Hence, the $(i,j)$th block of $A_t\times B_t$ is also the zero matrix for all $t=1,\ldots,r$. It follows that the corresponding block of their OR is zero as well. Suppose now that $A[i,j] = 1$. Here, the $(i,j)$th block of $A\otimes B$ is equal to the matrix $B$. On the other hand, the $(i,j)$th block of the matrix $\bigvee_{t=1}^r A_t\otimes B_t$ is precisely the OR of the matrices $B_t$ for which $A_t[i,j]= 1$. By assumption, these matrices form a cover of $B$. Hence, this block of the matrix $\bigvee_{t=1}^r A_t\otimes B_t$ is equal to $B$, as required. $\Box$

We also have the following converse of Lemma 3.

Lemma 4 ([4]): Let $A$ and $B$ be Boolean matrices. If $\rk{A\otimes B}=r$, then the pair $(A,B)$ has an $r$-cover consisting of only rank-$1$ matrices $A_1,\ldots,A_r$ and $B_1,\ldots,B_r$.

Proof: Let $\rk{A\otimes B}=r$. By the definition of $\rk{A\otimes B}$, there are rank-$1$ matrices $M_1,\ldots,M_r$ such that $A\otimes B=\bigvee_{t=1}^r M_t$. We will need one structural property of rectangles in Kronecker products of matrices.

Claim 1 ([4]): If $M\leq A\otimes B$ is a rank-$1$ matrix, then $M\leq M_A\otimes M_B$ for some rank-$1$ matrices $M_A\leq A$ and $M_B\leq B$.

Here is an illustration for Claim 1:

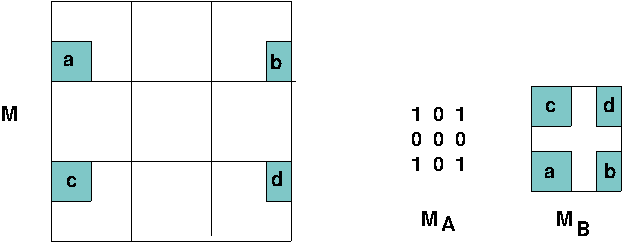
By Claim 1, for every $t$, there are rank-$1$ matrices $A_t\leq A$ and $B_t\leq B$ such that $M_t\leq A_t\otimes B_t$. Since $A_t\otimes B_t\leq A\otimes B$ holds for all $t$, we thus have $A\otimes B=\bigvee_{t=1}^r A_t\otimes B_t$, and it remains to show that these two sequences $A_1,\ldots,A_r$ and $B_1,\ldots,B_r$ of matrices form an $r$-cover of the pair $(A,B)$.

As before, the matrix $A\otimes B$ can be viewed as a matrix of blocks, where the block of $A\otimes B$ corresponding to the $(i,j)$ entry of matrix $A$ is $A[i,j]\cdot B$. The $(i,j)$th block of the matrix $A\otimes B$ is equal to the OR of the matrices $B_t$ for which $A_t[i,j]=1$. This implies that $A=\bigvee_{t=1}^r A_t$, because $A_t\leq A$ for all $t$, and because the blocks of $A\otimes B$ that correspond to $1$-entries of $A$ are equal to $B$. For the same reason, if $A[i,j] = 1$ then the matrices $B_t$ for which $A_t[i,j]=1$ form a cover of $B$, as required. $\Box$

In order to prove an upper bound on the OR-rank of $A\otimes B$ using Lemma 3, one has to find two sequences $A_1,\ldots,A_r$ and $B_1,\ldots,B_r$ of matrices forming a cover of the pair $(A,B)$. The following corollary gives a simple property of such families that suffices for this purpose.

Corollary 1: Let $A$ and $B$ be two Boolean matrices. Suppose that there exist two sequences $A_1,\ldots,A_s$ and $B_1,\ldots,B_s$ of Boolean matrices such that $A=\bigvee_{t\in T}A_t$ and $B=\bigvee_{t\in T}B_t$ holds for every subset $T\subseteq \{1,\ldots,s\}$ of size $|T|=\lceil s/2\rceil$. Then $\rk{A\otimes B}\leq \sum_{t=1}^r \rk{A_t\otimes B_t}$.

Proof: Clearly, the matrices $A_1,\ldots,A_s$ cover the matrix $A$, that is, $A=\bigvee_{t=1}^sA_t$ holds, because $A_t\leq A$ holds for every $t$. Next observe that for every $(i,j)$ such that $A[i,j]=1$, the number of matrices $A_t$ satisfying $A_t[i,j]=1$ is at least $\lceil s/2\rceil$. Indeed, if their number was smaller than $\lceil s/2\rceil$, then all the other matrices, whose number is larger than $s-\lceil s/2\rceil = \lfloor s/2\rfloor$, would have zeros in their $(i,j)$th entry, in contradiction to the assumption that they form a cover of $A$. It thus follows that for every $(i,j)$ such that $A[i,j]=1$, the number of matrices $B_t$ for which $B_t[i,j]=1$ is at least $\lceil s/2\rceil$. So, by our assumption, they cover the matrix $B$. This allows us to apply Lemma 3, and to complete the proof. $\Box$

The sum-rank, $\pr{A}$, of a (Boolean) matrix $A$ is the minimum number $r$ of rank-$1$ matrices $A_1,\ldots,A_r$ such that $A$ can be written as the sum $A=\sum_{t=1}^r A_t$ of these matrices. That is, if $A[i,j]=0$ then $A_t[i,j]=0$ for all $t$ (as before), but if $A[i,j]=1$ then $A_t[i,j]=1$ for exactly one $t$ (instead of for at least one $t$). In other words, we now have decompositions of $A$ into disjoint rectangles, instead of covers. Apparently, the following natural question remains open.

Open Problem: Does $\pr{A\otimes B}=\pr{A}\cdot\pr{B}$ hold?

^{2. If, say, rows of the matrix $A$ (not columns) have $\leq a$ zeros, then just consider random subsets $\J_1\subseteq C_A$ of columns of $A$, and similarly for the matrix $B$.  Jump back ☝}

References:

S. Jukna
Posted March 20, 2022.