A monotone coupling of distributions $\mu$ and $\nu$ on $\calx$ is a (joint) probability distribution $\theta$ on the Cartesian product $\calx\times\calx$ with marginal distributions $\mu$ and $\nu$: \begin{alignat}{2} \sum_{y\in\calx} \theta(x,y)&=\mu(x) && \phantom{aaaaaa}\mbox{for every $x\in\calx$} \label{eq:holley1a}\\ \sum_{x\in\calx} \theta(x,y)&=\nu(y) && \phantom{aaaaaa}\mbox{for every $y\in\calx$} \label{eq:holley2a}\\ \theta(x,y)&=0 &&\phantom{aaaaaa}\mbox{for all $(x,y)\not\in\Delta$,} \label{eq:holley3a} \end{alignat} where $\Delta:=\{(x,y)\in\calx\times\calx\colon x\Leq y\}$ is the set of all monotone pairs of elements.
Theorem [Strassen 1965] Let $(\calx,\Leq)$ be a partially ordered finite set, and $\mu,\nu$ be probability distributions on $\calx$. Then the following two assertions are equivalent.Proof: The (2) $\Leftarrow$ (1) direction is simple. Suppose that $\theta$ is a monotone coupling $\theta$ of $\mu$ and $\nu$. The upward closure of a set $A\subseteq \calx$ is the set $\Up{A}:=\{y\in\calx\colon \mbox{$x\Leq y$ for some $x\in A$}\}$. By the monotonicity of the coupling $\theta$, we have $\theta(x,y)=0$ for every $x\in\calx$ and $y\not\in\Up{\{x\}}$, as well as for every $y\in\calx$ and $x\not\in\Up{\{y\}}$. For every increasing set $A\subseteq \calx$, we have $\Up{A}=A$. Then for every increasing set $A\subseteq \calx$, we have: \begin{align*} \mu(A)&=\sum_{x\in A} \mu(x) = \sum_{x\in A}\sum_{y\in\calx}\theta(x,y)\\ &= \sum_{x\in A}\sum_{y\in\Up{\{x\}}}\theta(x,y)\\ &\leq\sum_{x\in A}\sum_{y\in \Up{A}} \theta(x,y) =\sum_{x\in A}\sum_{y\in A} \theta(x,y)\\ &=\sum_{y\in A} \sum_{x\in A} \theta(x,y)\\ &\leq \sum_{y\in A}\sum_{x\in\calx}\theta(x,y) =\sum_{y\in A} \nu(y)=\nu(A) \end{align*}
- $\mu\stLeq \nu$, that is, $\mu(A)\leq\nu(A)$ holds for every increasing set $A\subseteq \calx$
- There exists a monotone coupling $\theta$ of $\mu$ and $\nu$.
The (1) $\Leftarrow$ (2) direction is already nontrivial. Let $\mu$ and $\nu$ be probability distributions on $\calx$ such that $\mu\stLeq \nu$. It is enough to show that there exists a probability distribution $\theta$ on $\Delta$ satisfying both \eqref{eq:holley1a} and \eqref{eq:holley2a}.
Consider the set of functions $\theta:\calx\times\calx\to\RR$ satisfying the following system of linear inequalities and equalities: \begin{align} \theta_1(x)&:=\sum_{y\in\calx} \theta(x,y)\leq \mu(x) \qquad\mbox{for all $x\in\calx$;} \label{eq:strassen1} \\ \theta_2(y)&:=\sum_{x\in\calx} \theta(x,y) \leq \nu(y) \qquad \mbox{for all $y\in\calx$;} \label{eq:strassen2} \\ \theta(x,y)&\geq 0 \qquad\mbox{for all $x,y\in\calx$;} \label{eq:strassen3}\\ \theta(x,y)&=0 \qquad\mbox{for all $(x,y)\not\in\Delta$.} \label{eq:strassen4} \end{align} We search for the solution with the maximal $\ell_1$-norm (Manhattan norm): \[ \|\theta\|_1:=\sum_{x,y\in\calx}\theta(x,y) \to \max\,. \] Since our underlying set $\calx$ is finite, this is a linear programming task. Note that the first (as well as the second) constraint ensures that $\|\theta\|_1\leq 1$. The set of feasible solutions $\theta$ forms a compact subset of Euclidean space. Since $\theta\mapsto \|\theta\|_1$ is continuous, there exists an element of this set with $\|\theta\|_1$ maximal. This compact space is nonempty (at least, it includes the identically zero function), thus the maximum is reached. We take $\theta$ to be this maximal measure. We will show that in fact we must have $\|\theta\|_1=1$.
First, we inductively define sets $\{A_i\}$ and $\{B_i\}$: \begin{align*} A_1&=\{x\in\calx\colon \theta_1(x) < \mu(x)\}\,,\\ B_i&=\{y\in\calx\colon \mbox{there exists $x\in A_i$ with $x\Leq y$}\}\,,\\ A_{i+1}&=\{x\in\calx\colon \mbox{there exists $y\in B_i$ with $\theta(x,y)>0$}\}\,. \end{align*} Note that the inequality $\theta(x,y)>0$ yields $x\Leq y$ ($\theta$ can be nonzero only on pairs from $\Delta$). For us, it will be important that each set $B_i$ and, hence, also the entire set $B$ is an increasing set. (Recall that a set $B$ is increasing if $x\in B_i$ and $x\Leq y$ implies $y\in B_i$.) Indeed, if $y\in B_i$ then $x\Leq y$ for some $x\in A_i$ (by the definition of the set $B_i$). Now, if $y\Leq y'$, then also $x\Leq y'$ (by transitivity of $\Leq$); so, $y'$ also belongs to $B_i$.
Claim: $\theta_2(y)=\nu(y)$ for all $y\in B$.Proof: Suppose otherwise, in which case there must exist a $k$ and $y_k\in B$ with $\theta_2(y_k) < \nu(y_k)$. From the construction of the sets $\{A_i\}$ and $\{B_i\}$, there is a sequence $x_1,y_1,x_2,y_2,\ldots,x_k,y_k$ with $x_i\in A_i$ and $y_i\in B_i$ satisfying \begin{equation}\label{eq:strassen-construction} \theta_1(x_1) < \mu(x_1)\,,\qquad x_i\Leq y_i\,,\qquad \theta(x_{i},y_{i-1})>0\,,\qquad x_{i}\Leq y_{i-1}\,, \end{equation} where the relation $x_{i}\Leq y_{i-1}$ follows from $\theta(x_{i},y_{i-1})>0$ since $\theta$ can be nonzero only on monotone pairs.
Construction: Let us show how the desired sequence $x_1,y_1,x_2,y_2,\ldots,x_k,y_k$ can be constructed. Since $y_k\in B_k$, there is an $x_k\in A_k$ with $x_k\Leq y_k$. Since $x_k\in A_k$, there is an $y_{k-1}\in B_{k-1}$ such that $\theta(x_{k},y_{k-1})>0$. Since $\theta$ can be nonzero only on pairs from $\Delta$, we have $x_{k}\Leq y_{k-1}$. Since $y_{k-1}\in B_{k-1}$, there is an $x_{k-1}\in A_{k-1}$ with $x_{k-1}\Leq y_{k-1}$. Since $x_{k-1}\in A_{k-1}$, there is an $y_{k-2}\in B_{k-2}$ such that $\theta(x_{k-1},y_{k-2})>0$; hence, $x_{k-1}\Leq y_{k-2}$. Proceeding in this way we will construct a sequence $y_1,x_2,y_2,\ldots,x_k,y_k$. Finally, Since $y_1\in B_1$, there is a element $x_1\in A_1$ such that $x_1\Leq y_1$. Since $x_1\in A_1$, we also have that $\theta_1(x_1) < \mu(x_1)$.
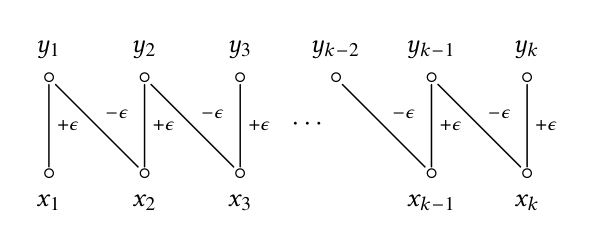
Take \[ \eps:= \min\big\{\mu(x_1)-\theta_1(x_1),\ \theta(x_2,y_1),\ \theta(x_3,y_2), \ldots, \theta(x_k,y_{k-1}),\ \nu(y_k)-\theta_2(y_k) \big\}\,. \] Note that all numbers is this minimum are positive; hence, $\eps>0$. Consider the perturbed function $\tilde{\theta}$ coinciding with $\theta$ everywhere, but with the following exceptions: \begin{align*} \tilde{\theta}(x_i,y_i)&=\theta(x_i,y_i)+\eps\ \ \ \ \mbox{for}\ \ \ \ i=1,2,\ldots,k\,;\\ \tilde{\theta}(x_i,y_{i-1})&=\theta(x_i,y_{i-1})-\eps \ \ \ \ \mbox{for}\ \ \ \ i=2,\ldots,k\,. \end{align*} The diagram below depicts the made perturbations when going from $\theta$ to $\tilde{\theta}$:

By \eqref{eq:strassen-constraints1} and \eqref{eq:strassen-constraints2}, $\tilde{\theta}$ satisfy all constraints \eqref{eq:strassen1}-\eqref{eq:strassen4} and, hence, is a feasible solution of our linear program. Yet, we have $\|\tilde{\theta}\|_1 > \|\theta\|_1$, because $\tilde{\theta}_1(x_1)=\theta_1(x_1)+\eps> \theta_1(x_1)$. This contradicts the maximality of $\theta$. $\Box$
Note that $\xbar{A}\subseteq \xbar{A}_1$, and that $\xbar{A}_1=\{x\in\calx\colon \theta_1(x) = \mu(x)\}$ by the definition of the set $A_1$; hence, $\theta_1(\xbar{A})=\mu(\xbar{A})$. We thus have \begin{align*} \theta_1(\xbar{A})+\theta_2(B) &= \mu(\xbar{A})+\nu(B) \quad\qquad\mbox{(by Claim 1)}\\ &\geq \mu(\xbar{A})+\mu(B) \quad\qquad\mbox{($B$ is increasing and $\mu\stLeq\nu$)}\\ &\geq \mu(\xbar{A})+\mu(A) \quad\qquad\mbox{(since $B\supseteq A$)}\\ &=1\,. \end{align*} On the other hand, \[ \theta_1(\xbar{A})+\theta_2(B) =\sum_{x\in\xbar{A}}\,\sum_{y\Geq x}\theta(x,y) +\sum_{y\in B}\,\sum_{x\Leq y}\theta(x,y) \leq \|\theta\|_1\,, \] because for all $x\in\xbar{A}$ and $y\in B$ we have $\theta(x,y)=0$: had we $x\Leq y$ for some $y\in B_i\subseteq B$, then $x$ would belong to $A_{i+1}\subseteq A$, not to $\xbar{A}$. This shows that $\|\theta\|_1=1$, i.e., $\theta$ defines a probability distribution. Together with \eqref{eq:strassen1} and \eqref{eq:strassen2}, this also gives $\theta_1(x)=\mu(x)$ and $\theta_2(y)=\nu_2(y)$ for all $x$ and $y$. $\Box$