This animation demonstrates the angular dispersion. At the begining of the animation spectrum of the nondispersed beam is depicted. At the end of the animation a linear angular dispersion is presented.

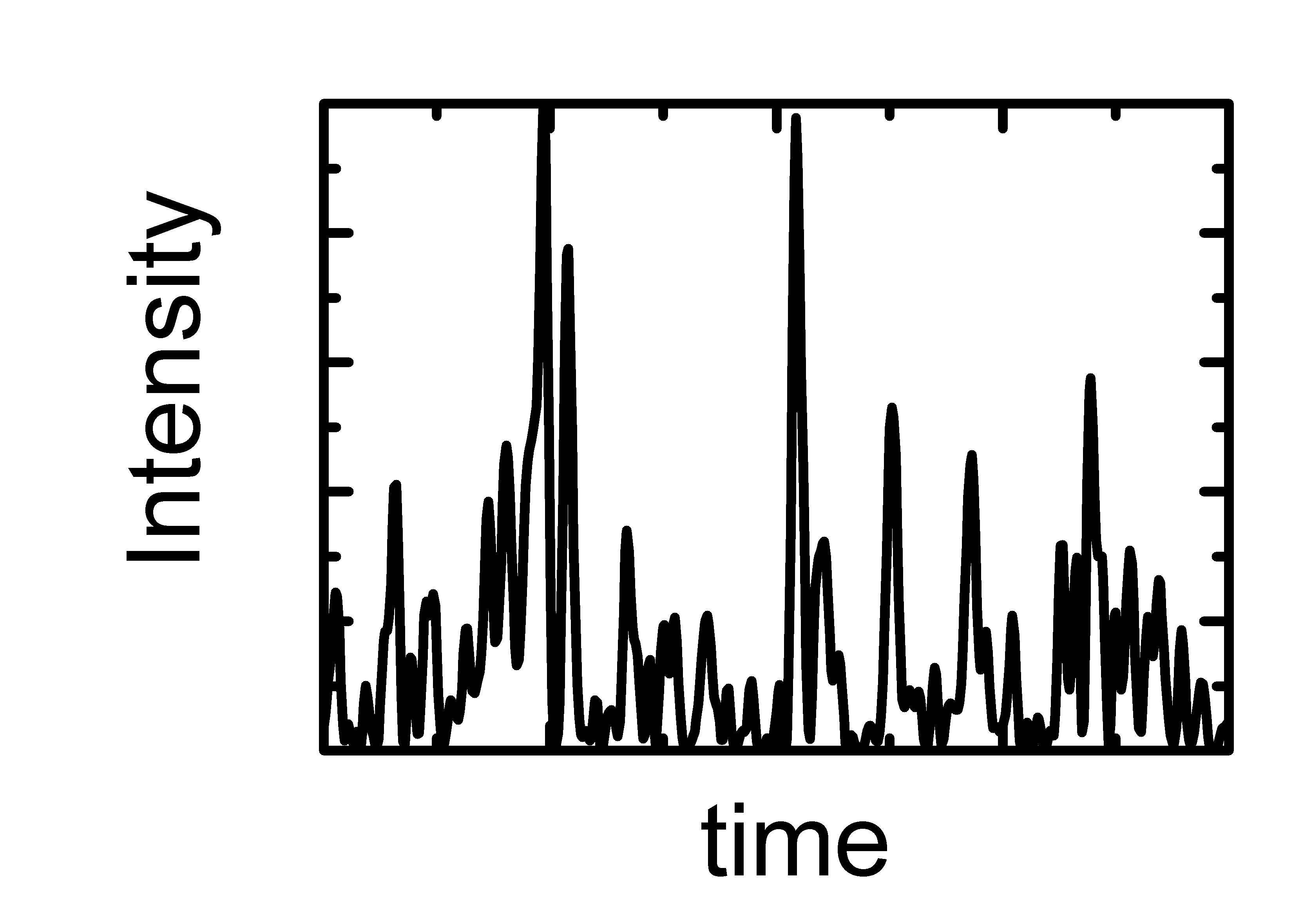
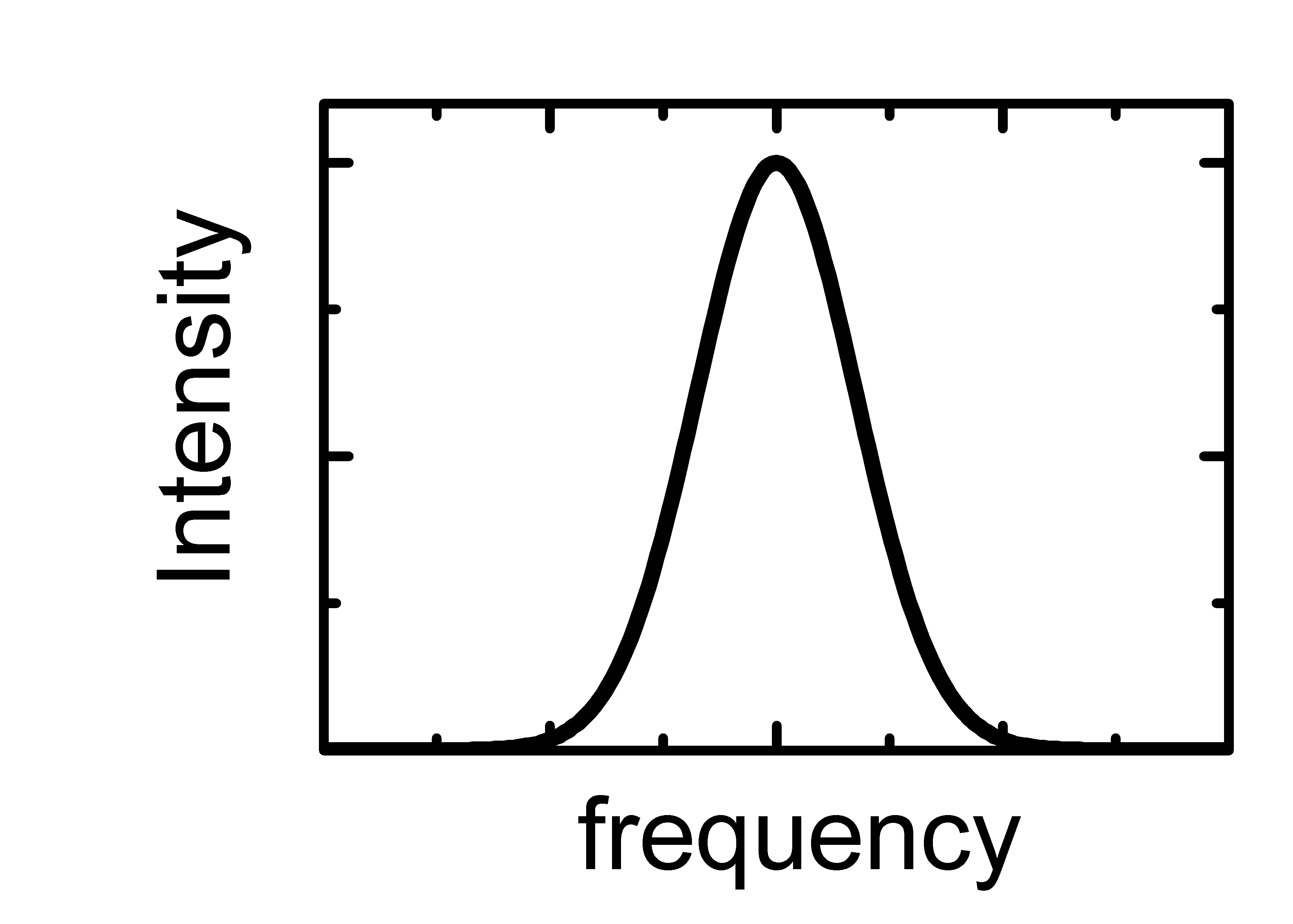
These two images show one realization of the Gaussian-Gaussian noise and its spectrum.

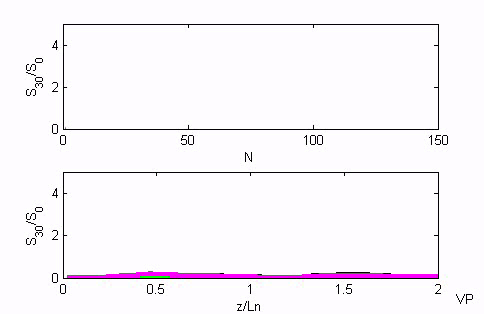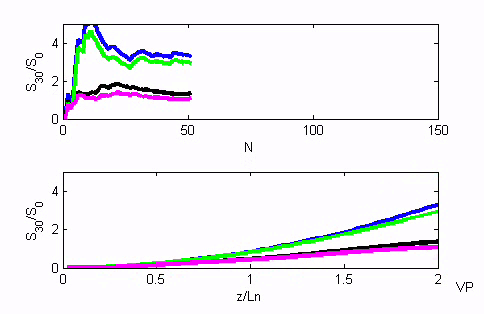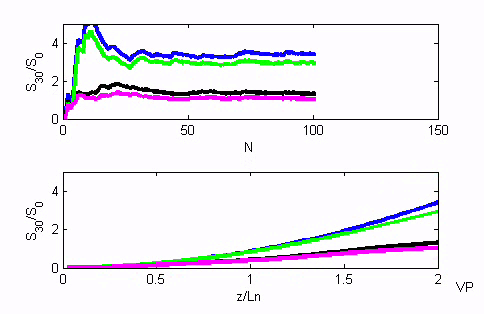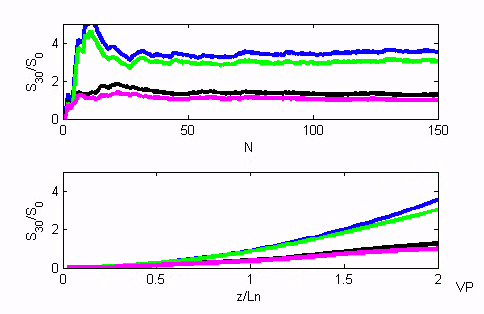
SECOND HARMONIC GENERATION (SHG) of incoherent wave. This animation shows the spectral radiance growth of the second harmonic generated from an incoherent wave. The theory is developed in [A. Piskarskas, V. Pyragaite, A. Stabinis, Generation of coherent waves by up- conversion and down-conversion of incoherent light, Phys. Rev. A 82, 053817 (11 pages) (2010)]. N is number of realizations, z/L_n - crystal length normalized to nonlinear interaction length. The nonlinear coupling equations were simulated in the cases of 1) the properly chosen angular dispersion (blue and green lines); 2) without angular dispersion (black and magenta lines). Linear (blue and black) and nonlinear (green and magenta) regimes are presented. The nonlinear interaction length is assumed to be rather small - 3 mm. For the conventional incoherent sources the nonlinear length is much larger and conversion efficiency is small. Still, we demonstrated theoretically the possibility to increase the growth of the spectral radiance with the properly chosen angular dispersion. In the case of the SHG it is linear.

This animation demonstrates the narrowing of the SH spectrum during propagation in nonlinear crystal.