Envelope bounds for tropical circuits

The situation with tropical circuits is more complicated. For every $A\subseteq\{0,1\}^n$, Lemma 1.34⁽⁴⁾ gives the lower bounds $\MMin{A}\geq \Un{\lenv{A}}$ and $\MMax{A}\geq \Un{\henv{A}}$, where $\lenv{A}$ consists of all vectors of $A$ smallest degree, and $\henv{A}$ consists of all vectors of $A$ largest degree. But what about other "envelopes" of $A$? Unfortunately, as mentioned in Remark 1.37⁽²⁾, already the gap $\Un{\henv{A}}/\MMin{A}$ can be even exponential. Still, also in the case of tropical circuits, we can prove high lower bounds by considering other, not necessarily lower or higher envelopes, as long as these envelopes have additional structural properties.

Arbitrary envelopes

• the degree $\nor{x}:=x_1+\cdots+x_n$ of vector $x$,
• the length $\nor{x}:=|\supp{x}|$ (the number of nonzero positions in $x$),
• $\nor{x}:=\skal{a,x}$ for a fixed vector $a\in\{0,1\}^n$.

As the norm measure of vectors $x\in \NN^n$, in this section we use their length \[ \length{x}:=|\supp{x}| \] (the number of nonzero entries of $x$). So, a rectangle $X+Y\subseteq \NN^n$ is locally $m$-balanced (under the length measure) if $m/3\leq |x|\leq 2m/3$ holds for all vectors $x\in X$. Recall that the upward closure $\Up{A}\subseteq\NN^n$ of a set $A\subseteq\NN^n$ of vectors consists of all vectors $b\in \NN^n$ such that $b\geq a$ for some $a\in A$, and the downward closure $\Down{A}\subseteq\NN^n$ of $A$ consists of all vectors $b\in \NN^n$ such that $b\leq a$ for some $a\in A$.

For a set $A\subseteq \NN^n$ of vectors, an integer $m\geq 2$ and the $m$-th envelope $B:=\{a\in A\colon |a|=m\}$ of $A$, let \[ \Rectbel{B}:=\max\left\{\big|(X+Y)\cap B\big|\colon \mbox{$X+Y\subseteq\Down{A}$ is locally $m$-balanced}\right\} \] denote the maximal possible number of vectors of $B$ contained in a locally $m$-balanced rectangle $X+Y$ lying below $A$. Note that we only know that rectangles $X+Y$ lie below the set $A$ (not necessarily $X+Y\subseteq A$): unlike it happens in the case of arithmetic and Minkowski circuits, the inclusion $X+Y\subseteq A$ does not need now to hold. Recall that a set $A$ of vectors is an antichain if $a\not\leq a'$ for all $a\neq a'\in A$.

Theorem A: Let $A\subseteq \{0,1\}^n$ be an antichain, $m\geq 3$ and $B=\{a\in A\colon |a|=m\}$ be the $m$-th envelope of $A$. Then there are $\MMax{A}$ or fewer locally $m$-balanced rectangles $X+Y$ lying below $A$ such that every vector $a\in B$ belongs to at least one of these rectangles. In particular, \[ \MMax{A}\geq \frac{|B|}{\Rectbel{B}}\,. \]

To show this lower bound, take an arbitrary locally $n$-balanced rectangle $X+Y\subseteq \Down{A}$ that contains the largest number of perfect matchings. Suppose that the rectangle $X+Y$ contains at least one perfect matching. We claim that then we actually have the inclusion \begin{equation}\label{eq:matchings1} X+Y \subseteq \Down{B}\,. \end{equation} Then, in particular, $(X+Y)\cap B=X+Y$ holds. To show this, take vectors $x_0\in X$ and $y_0\in Y$ such that $x_0+y_0$ is a perfect matching. Since $X+Y\subseteq \Down{A}$, for every vector $x_0+y$ with $y\in Y$ there is a vector $a\in A$ such that $x_0+y\leq a$ holds. But since the matching $x_0$ consists of $|x_0|\geq n/3 > 2$ vertex-disjoint edges, none of these vectors $a\in A$ can be a double-star. Hence, the rectangle $\{x_0\}+Y\subseteq\Down{B}$. In particular, all vectors $y\in Y$ are (characteristic $0$-$1$ vectors of) matchings. Similarly, by considering $y_0$ instead of $x_0$, we obtain that all vectors $x\in X$ must also be matchings. So, the entire rectangle $X+Y$ consists of only matchings, that is, $X+Y\subseteq\Down{B}$.

Thus, when applied to the set $B\subseteq A$ of all $|B|=n!$ perfect matchings, Theorem A, gives a lower bound $\MMax{A}\geq |B|/|X+Y|$, and it remains to show that $|X+Y|\leq n!\cdot 2^{-\Omega(n)}$. For this, let $r=|x_0|$ be the number of edges in the matching $x_0$; hence, $n/3\leq r\leq 2n/3$. Since $x_0+y_0$ is a perfect matching, the matching $y_0$ has $n-r$ edges. Since for every $x\in X$ and $y\in Y$ must be the characteristic $0$-$1$ vector of a matching, matchings $x\in X$ and $y\in Y$ must be vertex disjoint. A matching with $t$ edges can be contained in at most $(n-r)!$ perfect matchings. Hence, the number of perfect matchings in $X+Y$ is \[ |(X+Y)\cap B|\leq r!(n-r)!=n!\binom{n}{r}^{-1}=|B|\binom{n}{r}^{-1} \leq |B|\binom{n}{n/3}^{-1}\leq |B|3^{-n/3}\,, \] as desired.      $\Box$

Special envelopes

As the norm measure of vectors $x\in \NN^n$, in this section we again use their length \[ \length{x}:=|\supp{x}| \] (the number of nonzero entries). For example, the length of the vector $x=(5,0,3,8,0,1)$ is $\length{x}=4$. Thus, a rectangle $X+Y$ is locally $m$-balanced if $m/3\leq\length{x}\leq 2m/3$ holds for every vector $x\in X$. Such a rectangle $X+Y$ is strongly $m$-balanced if, additionally, $\length{x}=\length{x'}$ holds for all vectors $x,x'\in X$ (all vectors in $X$ have the same length lying between $m/3$ and $2m/3$).

For a set $A\subseteq \{0,1\}^n$ of vectors, an integer $m\geq 2$, and the $m$-th envelope $B:=\{a\in A\colon |a|=m\}$ of $A$, let \[ \Rect{B}:=\max\big\{|X+Y|\colon \mbox{$X+Y\subseteq B$ and $X+Y$ is strongly $m$-balanced}\big\} \] denote the maximal possible number $|X+Y|$ of vectors in a strongly $m$-balanced rectangle $X+Y\subseteq B$. Note that this time we even have the inclusion $X+Y\subseteq B$, not only $X+Y\subseteq\Down{A}$: unlike for the measure $\Rectbel{B}$, now the rectangles $X+Y$ cannot have any vectors from outside the set $B$.

Let $m\geq 2$ be an integer, $A\subseteq\{0,1\}^n$ be an antichain, and $B=\{a\in A\colon \length{a}=m\}$ be the $m$-th envelope of $A$. Having the parameter $m$ fixed, we call a vector $x\in\NN^n$ short if $\length{x}\lt m$, and long if $\length{x}\gt m$. A vector $x\in\NN^n$ is contained in a vector $y\in \NN^n$ if $x\leq y$, that is, if $x_i\leq y_i$ holds for all $i=1,\ldots,n$. The following lower bounds were proved in [1].

Theorem B:

1. If no short vector of $A$ is contained in any vector of $B + B$, then \[ \MMin{A} \geq \frac{|B|}{\Rect{B}}. \]
2. If no long vector of $A$ shares $m/3$ or more $1$s with any vector of $B$, then \[ \MMax{A} \geq \frac{|B|}{\Rect{B}}. \]

Proof: Suppose that an optimization problem (minimization or maximization) on $A$ can be solved by a tropical circuit of size $t$. Then, by Lemma 1.31⁽⁵⁾ (with "$C$" instead of "$B$"), there exists a set $C\subset\NN^n$ of vectors such that $\Un{C}\leq t$ (the set $C$ can be produced by a Minkowski $(\cup,+)$ circuit of size $\leq t$), the inclusion $A\subseteq C$ holds, and

1. either $B\subseteq A\subseteq C\subseteq \Up{A}$ in the case of $(\min,+)$ circuits

2. or $B\subseteq A\subseteq C\subseteq \Down{A}$ in the case of $(\max,+)$ circuits.

When applied with the norm measure $\nor{b}:=\length{b}$ (the length of vector $b$) and the "balance parameters" $r:=m$ and $\bal:=2/3$, Lemma 4.16⁽⁶⁾ gives us $\Un{C}\leq t$ locally $m$-balanced rectangles $X+Y\subseteq C$ such that every vector in $C$ of length at least $m$, and hence, also every vector $a\in B$ (since $B\subseteq C$), belongs to at least one of these rectangles.

So fix such a locally $m$-balanced rectangle $X+Y\subseteq C$. It is enough to show that the set $(X+Y)\cap B$ of vectors (which clearly lies in $B$) is either empty or there is a strongly $m$-balanced rectangle $X'+Y'$ such that \[ (X+Y)\cap B\subseteq X'+Y''\subseteq B\,. \] That is, the entire rectangle $X'+Y'$ lies in the set $B$, and every vector of $B$ that belongs to the rectangle $X+Y$ also belongs to the rectangle $X'+Y'$.

In general, if some two vectors $a+b$ and $x+y$ for $a,x\in X$ and $b,y\in Y$ belong to the set $B$ (a subset of $A$ and, hence, of $C$), then the "mixed" vectors $a+y$ and $x+b$ do not need to belong to the set $B$: we only know that these mixed vectors belong to the (apparently larger) set $C$. However, we additionally know that the set $C$ lies either above or below the set $A$. Together with the conditions (1) and (2) of Theorem B, this additional information about the set $C$ already ensures that the mixed vectors $a+y$ and $x+b$ must also belong to the set $B$. This is shown by the following claim.

Claim A: Let $a,x\in X$ and $b,y\in Y$ be such that both vectors $a+b$ and $x+y$ belong to $B$. Then (i) $\length{a}=\length{x}$, (ii) $\skal{a,y}=0$, and (iii) $a+y\in B$.

Case 1: $(\min,+)$ circuits; hence, $B\subseteq A\subseteq C\subseteq \Up{A}$. Our assumption in this case is that none of the short vectors of $A$ is contained in a vector of $B+B$. Since $C\subseteq \Up{A}$, and since the ``mixed'' vector $a+y$ belongs to $C$, there must be a vector $c\in A$ such that $a+y\geq c$. This yields \begin{equation}\label{eq:min-l} \length{a+y}\geq m\,. \end{equation} Indeed, if the vector $a+y$ were short (if $|\supp{a+y}|\lt m$ held) then $a+y\geq c$ would imply that the vector $c\in A$ would also be short. But then the sum $(a+b)+(x+y)\geq a+y$ of two vectors $a+b$ and $x+y$ of $B$ would contain a short vector $c$ of $A$, contradicting our assumption.

The property $\length{a}=\length{x}$ holds because, if $\length{a}\lt \length{x}$, then $\length{a+y}\leq \length{a}+\length{y}=\length{a}+(m-\length{x})\lt m$, a contradiction with Eq. \eqref{eq:min-l}. The orthogonality property $\skal{a,y}=0$ also holds because if $\skal{a,y}\neq 0$ held, then vectors $a$ and $y$ would share a common nonzero position, implying that $\length{a+y}\leq \length{a}+\length{y}-1=\length{x}+\length{y}-1=m-1$, and we again would obtain a contradiction with Eq. \eqref{eq:min-l}.

Now, since $\length{a}=\length{x}$ and $\skal{a,y}=0$, we have $\length{a+y}=\length{a}+\length{y} =\length{x}+\length{y}=m$. Together with $a+y\geq c$ and $\length{c}\geq m$, we have that $a+y=c$ and $\length{c}=m$. Since the set $B$ contains all vectors in $A$ of length $m$ (including vector $c$) this means that $a+y$ must belong to $B$, as desired.

Case 2: $(\max,+)$ circuits; hence, $B\subseteq A\subseteq C\subseteq \Down{A}$. Our assumption in this case is that no long vector of $A$ shares $m/3$ or more $1$s with any vector of $B$. Since $C\subseteq \Down{A}$, and the "mixed" vector $a+y$ belongs to $C$, there must be a vector $c\in A$ such that $a+y\leq c$. Since $c$ is a $0$-$1$ vector (it belongs to our set $A$ of $0$-$1$ vectors), the orthogonality property $\skal{a,y}=0$ trivially holds in this case. In particular, we have $\length{a+y}=\length{a}+\length{y}$. Since the rectangle $X+Y$ is locally $m$-balanced, and $a\in X$, we also know that $\length{a}\geq m/3$.

To show the equality $\length{a}=\length{x}$, assume for the sake of contradiction that $\length{a}\gt \length{x}$. Then $\length{a+y}= \length{a}+\length{y}=\length{a}+(m-\length{x}) \gt m$, meaning that $a+y$ is a long vector. Since $a+y\leq c$, vector $c\in A$ is then also a long vector. But then the scalar product $\skal{a+b,c}\geq \skal{a+b,a+y}\geq \length{a}\geq m/3$ of a vector $a+b$ in $B$ with a long vector $c$ in $A$ is not smaller than $m/3$, contradicting our assumption.

To show that $a+y\in B$, assume for the sake of contradiction that $a+y\not\in B$. Since $\skal{a,y}=0$ and $\length{a}=\length{x}$, the vector $a+y$ is a $0$-$1$ vector of length $\length{a}+\length{y}=\length{x}+\length{y}=m$. Since $B$ includes all vectors of $A$ of length $m$, and since $a+y\not\in B$, the vector $c\geq a+y$ of $A$ must be a long vector. But then, again, we have that the scalar product $\skal{a+b,c}$ of a vector $a+b$ in $B$ with a long vector $c$ in $A$ is not smaller than $m/3$, contradicting our assumption.

This finishes the proof of Claim A. ∎

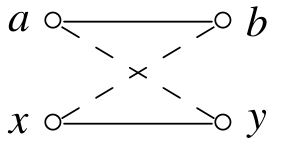
Now, given Claim A, we can finish the proof of Theorem B as follows. We have a locally $m$-balanced rectangle $X+Y\subseteq C$, and want to show that the set $(X+Y)\cap B$ of vectors is contained in some strongly $m$-balanced rectangle $\proj{X}+\proj{Y}$ lying entirely in the set $B$. For this, take \[ \proj{X}:=\{x\in X\colon (x+Y)\cap B\neq\emptyset\}\ \ \mbox{ and }\ \ \proj{Y}:=\{y\in Y\colon (X+y)\cap B\neq\emptyset\}\,. \] In terms of graphs, the sets $\proj{X}\subseteq X$ and $\proj{Y}\subseteq Y$ consist of all vertices of the complete bipartite graph $X\times Y$ that are non-isolated in the subgraph $G_B=\{(x,y)\in X\times Y\colon x+y\in B\}$ of $X\times Y$.

Consider the rectangle $\proj{X}+\proj{Y}\subseteq X+Y\subseteq C$. It is clear that the inclusion $(X+Y)\cap B\subseteq \proj{X}+\proj{Y}$ holds: if a vector $x+y$ with $x\in X$ and $y\in Y$ belongs to the set $B$, then vector $y$ "witnesses" the fact that vector $x$ belongs to $\proj{X}$, and vector $x$ "witnesses" the fact that vector $y$ belongs to $\proj{Y}$. On the other hand, by the definition of sets $\proj{X}$ and $\proj{Y}$, for every vectors $a,x\in \proj{X}$ and $b,y\in \proj{Y}$ there are vectors $x\in X$ and $b\in Y$ such that both vectors $a+b$ and $x+y$ belong to $B$. Then, by property (i) of Claim A we have $\length{a}=\length{x}$ and, by property (iii), both "mixed" vectors $a+y$ and $x+b$ also belong to the set $B$. Thus, the rectangle $\proj{X}+\proj{Y}$ is strongly $m$-balanced, and entirely lies in the set $B$, that is, the inclusions $(X+Y)\cap B\subseteq \proj{X}+\proj{Y}\subseteq B$ hold. Thus, every vector of $B$ that belongs the original rectangle $X+Y\subseteq C$ also belongs to the reduced rectangle $\proj{X}+\proj{Y}$ lying entirely in the set $B$. Since the $t$ original rectangles $X+Y\subseteq C$ contained all vectors of $B$, the inclusions imply that $B$ is contained in a union of the reduced rectangles $\proj{X}+\proj{Y} \subseteq B$, as desired.

This finishes the proof of Theorem B. ∎

Remark: In the proof of Theorem B, we applied Lemma 4.16⁽⁶⁾ with the balance parameter $\bal:=2/3$. Actually one can take any balance parameter satisfying $1/m\leq\bal \lt 1$. Then for every vectors $x\in X$ we will have inequalities $\bal m/2\leq \length{x}\leq \bal m$ instead of $m/3\leq\length{x}\leq 2m/3$.    $\Box$

In order to apply Theorem B to an optimization (minimization or maximization) problem on a given set $A\subseteq\{0,1\}^n$ of feasible solutions, one can consider the $m$-th envelope $B$ of $A$ for some chosen parameter $m$, and check whether condition (1) or (2) of Theorem B is fulfilled, and show that every strongly $m$-balanced rectangle $X+Y\subseteq B$ has at most some number $h$ of vectors: then $\MMin{A}\geq |B|/h$ in case (1), and $\MMax{A}\geq |B|/h$ in case (2).

Example 2: $(\min,+)$ circuits. Let $n \gt 3$, and consider the following minimization problem: given an assignment of nonnegative integer weights to the edges of $K_{n,n}$, find the minimum weight of a subgraph that is either a perfect matching or a $3$-star $K_{1,3}$.

The set $A$ of the characteristic $0$-$1$ vectors of feasible solutions of this $0/1$ minimization problem is the union $A=B\cup C$ of the set $B$ of characteristic $0$-$1$ vectors of all $|B|=n!$ perfect matchings, and $C$ is the set of characteristic $0$-$1$ vectors of all $|C|=n\binom{n}{3}=O(n^4)$ $3$-stars $K_{1,3}$ in $K_{n,n}$. Since $n \gt 3$, the lower envelope $\lenv{A}$ of $A$ is the set $C$ of $3$-stars. So, the lower bower bound $\MMin{A}\geq \Un{\lenv{A}}=\Un{C}$ given by Lemma 1.34⁽²⁾ in the book cannot yield any larger than $\Un{C}=O(n|C|)=O(n^4)$ lower bound on $\MMin{A}$. But Theorem B already yields an exponential lower bound $\MMin{A}=2^{\Omega(n)}$.

Since no $3$-star can be contained in a union of two perfect matchings, the first condition (1) of Theorem B (with $m:=n$) is fulfilled. The same argument as in the last paragraph of Example 1 shows that $|X+Y|\leq n!\cdot 2^{-\Omega(n)}= |B|\cdot 2^{-\Omega(n)}$ holds for every locally and, hence also for every strongly $n$-balanced rectangle $X+Y\subseteq B$. Since $|B|=n!$, the desired lower bound $\MMin{A}=2^{\Omega(n)}$ follows from Theorem B.      $\Box$

Example 3: $(\max,+)$ circuits. Consider the following maximization problem: given an assignment of nonnegative integer weights to the edges of $K_{n,n}$ for $n>6$, find the maximum weight of a subgraph that is either a perfect matching or a double-star $K_{2,n}$. The set $A$ of the characteristic $0$-$1$ vectors of feasible solutions of this $0/1$ minimization problem is the union $A=B\cup C$ of the set $B$ of characteristic $0$-$1$ vectors of all $|B|=n!$ perfect matchings, and $C$ is the set of characteristic $0$-$1$ vectors of all $|C|=\binom{n}{2}$ double-stars $K_{2,n}$ in $K_{n,n}$. Since the upper envelope $\henv{A}$ of $A$ is the set $C$ of double-stars, the lower bower bound $\MMax{A}\geq \Un{\henv{A}}=\Un{C}$ given by Lemma 1.34⁽²⁾ cannot yield any larger than $\Un{C}=O(n^2)$ lower bound on $\MMax{A}$.

In Example 1, we have used Theorem A to show that still an exponential lower bound $\MMax{A}=2^{\Omega(n)}$ holds. The main step was to show that if a rectangle $X+Y\subseteq\Down{A}$, and if it contains at least one perfect matching, then $X+Y\subseteq\Down{B}$ holds, that is, every vector $x+y$ of $X+Y$ is the characteristic $0$-$1$ vector of matching. Using Theorem B, we can give an alternative proof of this lower bound.

As in Example 2, we will apply Theorem B with $m:=n$. Then the set $B$ (of perfect matchings) is the $n$-th envelope of $A$, and long vectors of $A$ (those with $\gt n$ ones) are exactly the vectors of $C$ (double-stars). Since no double-star can share more than two edges with a perfect matching and since $n\gt 6$, the second condition (2) of Theorem B is fulfilled. The same argument in the last paragraph of Example 1 gives an upper bound $|X+Y|\leq n!\cdot \binom{n}{n/3}^{-1} = |B|\cdot \binom{n}{n/3}^{-1}\leq |B|\cdot 3^{-n/3}$. Thus, Theorem B yields $\MMax{A}\geq |B|/|X+Y|\geq 3^{-n/3}$.      $\Box$

Footnotes

^{(1)   Jump back ☝}

---

^{(2)   Jump back ☝}

---

^{(3)   Jump back ☝}

---

^{(4)   Jump back ☝}

---

^{(5)   Jump back ☝}

---

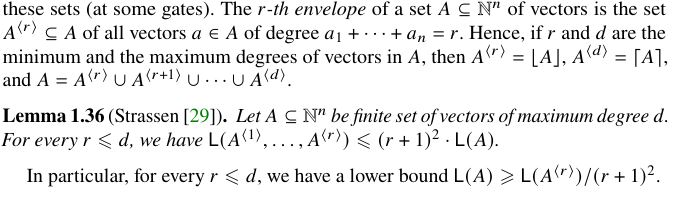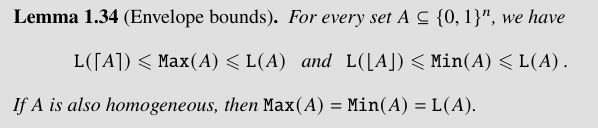^{(6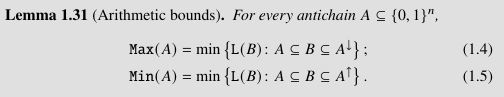)   Jump back ☝}

---

References:

1. Jukna, S.: Tropical complexity, Sidon sets and dynamic programming. SIAM J. Discrete Math. 30(4), 2064–2085 (2016)   local copy