\(
\def\<#1>{\left<#1\right>}
\let\geq\geqslant
\let\leq\leqslant
% an undirected version of \rightarrow:
\newcommand{\mathdash}{\relbar\mkern-9mu\relbar}
\def\deg#1{\mathrm{deg}(#1)}
\newcommand{\dg}[1]{d_{#1}}
\newcommand{\Norm}{\mathrm{N}}
\newcommand{\const}[1]{c_{#1}}
\newcommand{\cconst}[1]{\alpha_{#1}}
\newcommand{\Exp}[1]{E_{#1}}
\newcommand*{\ppr}{\mathbin{\ensuremath{\otimes}}}
\newcommand*{\su}{\mathbin{\ensuremath{\oplus}}}
\newcommand{\nulis}{\vmathbb{0}} %{\mathbf{0}}
\newcommand{\vienas}{\vmathbb{1}}
\newcommand{\Up}[1]{#1^{\uparrow}} %{#1^{\vartriangle}}
\newcommand{\Down}[1]{#1^{\downarrow}} %{#1^{\triangledown}}
\newcommand{\lant}[1]{#1_{\mathrm{la}}} % lower antichain
\newcommand{\uant}[1]{#1_{\mathrm{ua}}} % upper antichain
\newcommand{\skal}[1]{\langle #1\rangle}
\newcommand{\NN}{\mathbb{N}} % natural numbers
\newcommand{\RR}{\mathbb{R}}
\newcommand{\minTrop}{\mathbb{T}_{\mbox{\rm\footnotesize min}}}
\newcommand{\maxTrop}{\mathbb{T}_{\mbox{\rm\footnotesize max}}}
\newcommand{\FF}{\mathbb{F}}
\newcommand{\pRR}{\mathbb{R}_{\mbox{\tiny $+$}}}
\newcommand{\QQ}{\mathbb{Q}}
\newcommand{\ZZ}{\mathbb{Z}}
\newcommand{\gf}[1]{GF(#1)}
\newcommand{\conv}[1]{\mathrm{Conv}(#1)}
\newcommand{\vvec}[2]{\vec{#1}_{#2}}
\newcommand{\f}{{\mathcal F}}
\newcommand{\h}{{\mathcal H}}
\newcommand{\A}{{\mathcal A}}
\newcommand{\B}{{\mathcal B}}
\newcommand{\C}{{\mathcal C}}
\newcommand{\R}{{\mathcal R}}
\newcommand{\MPS}[1]{f_{#1}} % matrix multiplication
\newcommand{\ddeg}[2]{\#_{#2}(#1)}
\newcommand{\length}[1]{|#1|}
\DeclareMathOperator{\support}{sup}
\newcommand{\supp}[1]{\support(#1)}
\DeclareMathOperator{\Support}{sup}
\newcommand{\spp}{\Support}
\newcommand{\Supp}[1]{\mathrm{Sup}(#1)} %{\mathcal{S}_{#1}}
\newcommand{\lenv}[1]{\lfloor #1\rfloor}
\newcommand{\henv}[1]{\lceil#1\rceil}
\newcommand{\homm}[2]{{#1}^{\langle #2\rangle}}
\let\daug\odot
\let\suma\oplus
\newcommand{\compl}[1]{Y_{#1}}
\newcommand{\pr}[1]{X_{#1}}
\newcommand{\xcompl}[1]{Y'_{#1}}
\newcommand{\xpr}[1]{X'_{#1}}
\newcommand{\cont}[1]{A_{#1}} % content
\def\fontas#1{\mathsf{#1}} %{\mathrm{#1}} %{\mathtt{#1}} %
\newcommand{\arithm}[1]{\fontas{Arith}(#1)}
\newcommand{\Bool}[1]{\fontas{Bool}(#1)}
\newcommand{\linBool}[1]{\fontas{Bool}_{\mathrm{lin}}(#1)}
\newcommand{\rBool}[2]{\fontas{Bool}_{#2}(#1)}
\newcommand{\BBool}[2]{\fontas{Bool}_{#2}(#1)}
\newcommand{\MMin}[1]{\fontas{Min}(#1)}
\newcommand{\MMax}[1]{\fontas{Max}(#1)}
\newcommand{\negMin}[1]{\fontas{Min}^{-}(#1)}
\newcommand{\negMax}[1]{\fontas{Max}^{-}(#1)}
\newcommand{\Min}[2]{\fontas{Min}_{#2}(#1)}
\newcommand{\Max}[2]{\fontas{Max}_{#2}(#1)}
\newcommand{\convUn}[1]{\fontas{L}_{\ast}(#1)}
\newcommand{\Un}[1]{\fontas{L}(#1)}
\newcommand{\kUn}[2]{\fontas{L}_{#2}(#1)}
\newcommand{\Nor}{\mu} % norm without argument
\newcommand{\nor}[1]{\Nor(#1)}
\newcommand{\bool}[1]{\hat{#1}} % Boolean version of f
\newcommand{\bphi}{\phi} % boolean circuit
\newcommand{\xf}{\boldsymbol{\mathcal{F}}}
\newcommand{\euler}{\mathrm{e}}
\newcommand{\ee}{f} % other element
\newcommand{\exchange}[3]{{#1}-{#2}+{#3}}
\newcommand{\dist}[2]{{#2}[#1]}
\newcommand{\Dist}[1]{\mathrm{dist}(#1)}
\newcommand{\mdist}[2]{\dist{#1}{#2}} % min-max dist.
\newcommand{\matching}{\mathcal{M}}
\renewcommand{\E}{A}
\newcommand{\F}{\mathcal{F}}
\newcommand{\set}{W}
\newcommand{\Deg}[1]{\mathrm{deg}(#1)}
\newcommand{\mtree}{MST}
\newcommand{\stree}{{\cal T}}
\newcommand{\dstree}{\vec{\cal T}}
\newcommand{\Rich}{U_0}
\newcommand{\Prob}[1]{\ensuremath{\mathrm{Pr}\left\{{#1}\right\}}}
\newcommand{\xI}{\boldsymbol{I}}
\newcommand{\plus}{\mbox{\tiny $+$}}
\newcommand{\sgn}[1]{\left[#1\right]}
\newcommand{\ccompl}[1]{{#1}^*}
\newcommand{\contr}[1]{[#1]}
\newcommand{\harm}[2]{{#1}\,\#\,{#2}} %{{#1}\,\oplus\,{#2}}
\newcommand{\hharm}{\#} %{\oplus}
\newcommand{\rec}[1]{1/#1}
\newcommand{\rrec}[1]{{#1}^{-1}}
\DeclareRobustCommand{\bigO}{%
\text{\usefont{OMS}{cmsy}{m}{n}O}}
\newcommand{\dalyba}{/}%{\oslash}
\newcommand{\mmax}{\mbox{\tiny $\max$}}
\newcommand{\thr}[2]{\mathrm{Th}^{#1}_{#2}}
\newcommand{\rectbound}{h}
\newcommand{\pol}[3]{\sum_{#1\in #2}{#3}_{#1}\prod_{i=1}^n x_i^{#1_i}}
\newcommand{\tpol}[2]{\min_{#1\in #2}\left\{\skal{#1,x}+\const{#1}\right\}}
\newcommand{\comp}{\circ} % composition
\newcommand{\0}{\vec{0}}
\newcommand{\drops}[1]{\tau(#1)}
\newcommand{\HY}[2]{F^{#2}_{#1}}
\newcommand{\hy}[1]{f_{#1}}
\newcommand{\hh}{h}
\newcommand{\hymin}[1]{f_{#1}^{\mathrm{min}}}
\newcommand{\hymax}[1]{f_{#1}^{\mathrm{max}}}
\newcommand{\ebound}[2]{\partial_{#2}(#1)}
\newcommand{\Lpure}{L_{\mathrm{pure}}}
\newcommand{\Vpure}{V_{\mathrm{pure}}}
\newcommand{\Lred}{L_1} %L_{\mathrm{red}}}
\newcommand{\Lblue}{L_0} %{L_{\mathrm{blue}}}
\newcommand{\epr}[1]{z_{#1}}
\newcommand{\wCut}[1]{w(#1)}
\newcommand{\cut}[2]{w_{#2}(#1)}
\newcommand{\Length}[1]{l(#1)}
\newcommand{\Sup}[1]{\mathrm{Sup}(#1)}
\newcommand{\ddist}[1]{d_{#1}}
\newcommand{\sym}[2]{S_{#1,#2}}
\newcommand{\minsum}[2]{\mathrm{MinS}^{#1}_{#2}}
\newcommand{\maxsum}[2]{\mathrm{MaxS}^{#1}_{#2}} % top k-of-n function
\newcommand{\cirsel}[2]{\Phi^{#1}_{#2}} % its circuit
\newcommand{\sel}[2]{\sym{#1}{#2}} % symmetric pol.
\newcommand{\cf}[1]{{#1}^{o}}
\newcommand{\Item}[1]{\item[\mbox{\rm (#1)}]} % item in roman
\newcommand{\bbar}[1]{\underline{#1}}
\newcommand{\Narrow}[1]{\mathrm{Narrow}(#1)}
\newcommand{\Wide}[1]{\mathrm{Wide}(#1)}
\newcommand{\eepsil}{\varepsilon}
\newcommand{\amir}{\varphi}
\newcommand{\mon}[1]{\mathrm{mon}(#1)}
\newcommand{\mmon}{\alpha}
\newcommand{\gmon}{\alpha}
\newcommand{\hmon}{\beta}
\newcommand{\nnor}[1]{\|#1\|}
\newcommand{\inorm}[1]{\left\|#1\right\|_{\mbox{\tiny $\infty$}}}
\newcommand{\mstbound}{\gamma}
\newcommand{\coset}[1]{\textup{co-}{#1}}
\newcommand{\spol}[1]{\mathrm{ST}_{#1}}
\newcommand{\cayley}[1]{\mathrm{C}_{#1}}
\newcommand{\SQUARE}[1]{\mathrm{SQ}_{#1}}
\newcommand{\STCONN}[1]{\mathrm{STCON}_{#1}}
\newcommand{\STPATH}[1]{\mathrm{PATH}_{#1}}
\newcommand{\SSSP}[1]{\mathrm{SSSP}(#1)}
\newcommand{\APSP}[1]{\mathrm{APSP}(#1)}
\newcommand{\MP}[1]{\mathrm{MP}_{#1}}
\newcommand{\CONN}[1]{\mathrm{CONN}_{#1}}
\newcommand{\PERM}[1]{\mathrm{PER}_{#1}}
\newcommand{\mst}[2]{\tau_{#1}(#2)}
\newcommand{\MST}[1]{\mathrm{MST}_{#1}}
\newcommand{\MIS}{\mathrm{MIS}}
\newcommand{\dtree}{\mathrm{DST}}
\newcommand{\DST}[1]{\dtree_{#1}}
\newcommand{\CLIQUE}[2]{\mathrm{CL}_{#1,#2}}
\newcommand{\ISOL}[1]{\mathrm{ISOL}_{#1}}
\newcommand{\POL}[1]{\mathrm{POL}_{#1}}
\newcommand{\ST}[1]{\ptree_{#1}}
\newcommand{\Per}[1]{\mathrm{per}_{#1}}
\newcommand{\PM}{\mathrm{PM}}
\newcommand{\error}{\epsilon}
\newcommand{\PI}[1]{A_{#1}}
\newcommand{\Low}[1]{A_{#1}}
\newcommand{\node}[1]{v_{#1}}
\newcommand{\BF}[2]{W_{#2}[#1]} % Bellman-Ford
\newcommand{\FW}[3]{W_{#1}[#2,#3]} % Floyd-Washall
\newcommand{\HK}[1]{W[#1]} % Held-Karp
\newcommand{\WW}[1]{W[#1]}
\newcommand{\pWW}[1]{W^{+}[#1]}
\newcommand{\nWW}[1]{W^-[#1]}
\newcommand{\knap}[2]{W_{#2}[#1]}
\newcommand{\Cut}[1]{w(#1)}
\newcommand{\size}[1]{\mathrm{size}(#1)}
\newcommand{\dual}[1]{{#1}^{\ast}}
\def\gcd#1{\mathrm{gcd}(#1)}
\newcommand{\econt}[1]{C_{#1}}
\newcommand{\xecont}[1]{C_{#1}'}
\newcommand{\rUn}[1]{\fontas{L}_{r}(#1)}
\newcommand{\copath}{\mathrm{co}\text{-}\mathrm{Path}_n}
\newcommand{\Path}{\mathrm{Path}_n}
\)
Can the Max(A)/Min(A) gap be large in approximation?
-
As in the book, for a finite set $A\subseteq \NN^n$ of feasible solutions, $\Min{A}{r}$ and $\Max{A}{r}$
denote, respectively, the minimum size of a $(\min,+)$ and of a $(\max,+)$ circuit approximating the minimization problem $f(x)=\min_{a\in A}\skal{a,x}$, resp., the maximization problem
$f(x)=\max_{a\in A}\skal{a,x}$
on a given set $A\subseteq \NN^n$ of feasible solution with the factor $r$.
We already know that for homogeneous sets $A\subseteq \{0,1\}^n$ (all vectors have the same number of $1$s) the equalities $\Max{A}{1}=\Min{A}{1}=\Un{A}$ hold (Lemma 1.34(1)).
The situation, however, is entirely different if we consider
approximating circuits: when treating families $\f\subseteq 2^{[n]}$
as sets $A\subseteq \{0,1\}^n$ of their characteristic $0$-$1$ vectors, Corollary 4.13(2) gives
us doubly-exponentially many in $n$ homogeneous sets $A\subseteq\{0,1\}^n$ such that
the gap $\Min{A}{r}/\Max{A}{s}$ is exponential for already $s=1+o(1)$ and for arbitrary large factors $r\geq 1$.
But what about
converse gaps, Max/Min gaps?
Problem A:
Do there exist antichains $A\subseteq\{0,1\}^n$ for which the gap
$\Max{A}{r}/\Min{A}{s}$ is super-polynomial for some $r\geq s>1$?
Remark 1 (Antichains):
The requirement that the separating set $A$ must be an antichain
is to exclude trivial separations. Indeed,
otherwise
the gap
could be artificially made large. To see this, take an arbitrary
$m$-homogeneous set $B\subseteq\{0,1\}^n$ (all vectors of $A$ have the same number $m\gt 1$ of ones) for which $\Max{B}{r}$ is large (as in
Corollary 4.24(3), for example). The set $B$ is an antichain. Extend it to
a non-antichain $A=B\cup\{\vec{e}_1,\cdots,\vec{e}_n\}$. Then
$\Max{A}{r}$ still remains large (since input weightings $x\in\RR^n_+$ are nonnegative, the maximization problems of both sets $A$ and $B$ are equivalent) but
$\Min{A}{1}\leq n$ holds (just output $\min\{x_1,\ldots,x_n\}$).
$\Box$
Remark 2 (Approximation factors):
A vector $b\in\NN^n$ is contained in a vector $a\in\NN^n$ if $b\leq a$ holds. A set $A\subseteq\{0,1\}^n$ is $m$-bounded if no its vector has more than $m$ ones, and is
$k$-dense if every vector $b\in \{0,1\}^n$ with $k$ ones is contained in at least one vector of $A$. In particular, every set $A\subseteq\{0,1\}^n$ is $m$-bounded for $m=n$, and is $k$-dense for $k=1$
(as long as there is no position in which all vectors of $A$ have $0$; then just take smaller dimension $n$).
Proposition 4.11
in the book shows that for every such set $A$, we have $\Max{A}{r}=O(nk)$ already for the factor $r=m/k$. So, the gap $\Max{A}{r}/\Min{A}{s}$ can only be large (if at all) for approximation factors $r\lt m/k$.
$\Box$
Remark 3:
Note that to have $\Min{A}{s}$ "small", it is necessary (albeit not sufficient) that the Boolean version $g(x)=\bigvee_{a\in A}\bigwedge_{i\in\supp{a}}x_i$ of the minimization problem $f(x)=\min_{a\in A}\skal{a,x}$ of the set $A$ has "small monotone Boolean $(\lor,\land)$ circuits: by Lemma 1.30 in the book, the lower bound
$\Min{A}{s}\geq \Bool{A}$ holds for every antichain $A\subseteq\{0,1\}^n$ and arbitrary large (but finite) approximation factors $r\geq 1$.
$\Box$
Let us now look at the set $P_n$ of characteristic $0$-$1$ vectors of all $s$-$t$ paths in $K_m$, where $n=\binom{m}{2}$. The Bellman-Ford-Moore $(\min,+)$ circuit yields $\Min{P_n}{s}=O(n^{3/2})$ already for the factor $s=1$ (exact solving).
On the other hand, the maximization problem on the set $P_n$ is the
well-known longest $s$-$t$ path problem in $K_m$. This already is a hard problem (via reduction to Hamiltonian paths). But can we prove (without relying on the unproven as yet inequality $P\neq NP$) that this latter maximization problem is hard to approximate by poly-size $(\max,+)$ circuits within the factor, say, $r=2$?
Problem B:
Prove that $\Max{P_n}{2}$ is super-polynomial.
A related question is: can the maximization problem on $P_n$ be approximated within any non-trivial factor $r$ by poly-size $(\max,+)$ circuits?
Problem C:
Is $\Max{P_n}{r}$ polynomial for some factor $r\lt (m-1)/2$?
This "strange" condition $r\lt (m-1)/2$ on the approximation factor $r$
comes from Remark 2. The set $P_n$ is $(m-1)$-bounded (no $s$-$t$ path in $K_m$ has more than $m-1$ edges), and is $k$-dense for $k=2$ (every two edges of $K_m$
lie in at least one such path). Hence, factors $r\geq (m-1)/2$ are not interesting for the maximization problem on $P_n$.
Footnotes:
(1)
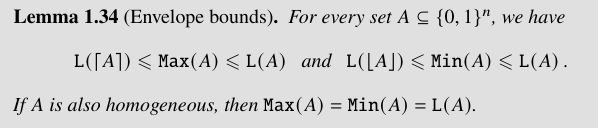 Jump back ☝
Jump back ☝
(2)
 Jump back ☝
Jump back ☝
(3)
 Jump back ☝
Jump back ☝
⇦ Back to the comments page
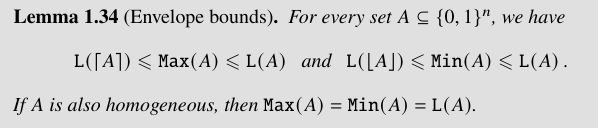 Jump back ☝
Jump back ☝
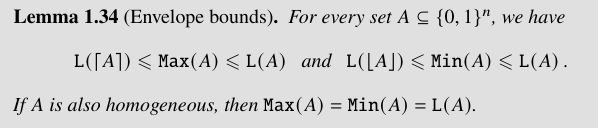 Jump back ☝
Jump back ☝
 Jump back ☝
Jump back ☝
 Jump back ☝
Jump back ☝