\(
\def\<#1>{\left<#1\right>}
\let\geq\geqslant
\let\leq\leqslant
% an undirected version of \rightarrow:
\newcommand{\mathdash}{\relbar\mkern-9mu\relbar}
\def\deg#1{\mathrm{deg}(#1)}
\newcommand{\dg}[1]{d_{#1}}
\newcommand{\Norm}{\mathrm{N}}
\newcommand{\const}[1]{c_{#1}}
\newcommand{\cconst}[1]{\alpha_{#1}}
\newcommand{\Exp}[1]{E_{#1}}
\newcommand*{\ppr}{\mathbin{\ensuremath{\otimes}}}
\newcommand*{\su}{\mathbin{\ensuremath{\oplus}}}
\newcommand{\nulis}{\vmathbb{0}} %{\mathbf{0}}
\newcommand{\vienas}{\vmathbb{1}}
\newcommand{\Up}[1]{#1^{\uparrow}} %{#1^{\vartriangle}}
\newcommand{\Down}[1]{#1^{\downarrow}} %{#1^{\triangledown}}
\newcommand{\lant}[1]{#1_{\mathrm{la}}} % lower antichain
\newcommand{\uant}[1]{#1_{\mathrm{ua}}} % upper antichain
\newcommand{\skal}[1]{\langle #1\rangle}
\newcommand{\NN}{\mathbb{N}} % natural numbers
\newcommand{\RR}{\mathbb{R}}
\newcommand{\minTrop}{\mathbb{T}_{\mbox{\rm\footnotesize min}}}
\newcommand{\maxTrop}{\mathbb{T}_{\mbox{\rm\footnotesize max}}}
\newcommand{\FF}{\mathbb{F}}
\newcommand{\pRR}{\mathbb{R}_{\mbox{\tiny $+$}}}
\newcommand{\QQ}{\mathbb{Q}}
\newcommand{\ZZ}{\mathbb{Z}}
\newcommand{\gf}[1]{GF(#1)}
\newcommand{\conv}[1]{\mathrm{Conv}(#1)}
\newcommand{\vvec}[2]{\vec{#1}_{#2}}
\newcommand{\f}{{\mathcal F}}
\newcommand{\h}{{\mathcal H}}
\newcommand{\A}{{\mathcal A}}
\newcommand{\B}{{\mathcal B}}
\newcommand{\C}{{\mathcal C}}
\newcommand{\R}{{\mathcal R}}
\newcommand{\MPS}[1]{f_{#1}} % matrix multiplication
\newcommand{\ddeg}[2]{\#_{#2}(#1)}
\newcommand{\length}[1]{|#1|}
\DeclareMathOperator{\support}{sup}
\newcommand{\supp}[1]{\support(#1)}
\DeclareMathOperator{\Support}{sup}
\newcommand{\spp}{\Support}
\newcommand{\Supp}[1]{\mathrm{Sup}(#1)} %{\mathcal{S}_{#1}}
\newcommand{\lenv}[1]{\lfloor #1\rfloor}
\newcommand{\henv}[1]{\lceil#1\rceil}
\newcommand{\homm}[2]{{#1}^{\langle #2\rangle}}
\let\daug\odot
\let\suma\oplus
\newcommand{\compl}[1]{Y_{#1}}
\newcommand{\pr}[1]{X_{#1}}
\newcommand{\xcompl}[1]{Y'_{#1}}
\newcommand{\xpr}[1]{X'_{#1}}
\newcommand{\cont}[1]{A_{#1}} % content
\def\fontas#1{\mathsf{#1}} %{\mathrm{#1}} %{\mathtt{#1}} %
\newcommand{\arithm}[1]{\fontas{Arith}(#1)}
\newcommand{\Bool}[1]{\fontas{Bool}(#1)}
\newcommand{\linBool}[1]{\fontas{Bool}_{\mathrm{lin}}(#1)}
\newcommand{\rBool}[2]{\fontas{Bool}_{#2}(#1)}
\newcommand{\BBool}[2]{\fontas{Bool}_{#2}(#1)}
\newcommand{\MMin}[1]{\fontas{Min}(#1)}
\newcommand{\MMax}[1]{\fontas{Max}(#1)}
\newcommand{\negMin}[1]{\fontas{Min}^{-}(#1)}
\newcommand{\negMax}[1]{\fontas{Max}^{-}(#1)}
\newcommand{\Min}[2]{\fontas{Min}_{#2}(#1)}
\newcommand{\Max}[2]{\fontas{Max}_{#2}(#1)}
\newcommand{\convUn}[1]{\fontas{L}_{\ast}(#1)}
\newcommand{\Un}[1]{\fontas{L}(#1)}
\newcommand{\kUn}[2]{\fontas{L}_{#2}(#1)}
\newcommand{\Nor}{\mu} % norm without argument
\newcommand{\nor}[1]{\Nor(#1)}
\newcommand{\bool}[1]{\hat{#1}} % Boolean version of f
\newcommand{\bphi}{\phi} % boolean circuit
\newcommand{\xf}{\boldsymbol{\mathcal{F}}}
\newcommand{\euler}{\mathrm{e}}
\newcommand{\ee}{f} % other element
\newcommand{\exchange}[3]{{#1}-{#2}+{#3}}
\newcommand{\dist}[2]{{#2}[#1]}
\newcommand{\Dist}[1]{\mathrm{dist}(#1)}
\newcommand{\mdist}[2]{\dist{#1}{#2}} % min-max dist.
\newcommand{\matching}{\mathcal{M}}
\renewcommand{\E}{A}
\newcommand{\F}{\mathcal{F}}
\newcommand{\set}{W}
\newcommand{\Deg}[1]{\mathrm{deg}(#1)}
\newcommand{\mtree}{MST}
\newcommand{\stree}{{\cal T}}
\newcommand{\dstree}{\vec{\cal T}}
\newcommand{\Rich}{U_0}
\newcommand{\Prob}[1]{\ensuremath{\mathrm{Pr}\left\{{#1}\right\}}}
\newcommand{\xI}{\boldsymbol{I}}
\newcommand{\plus}{\mbox{\tiny $+$}}
\newcommand{\sgn}[1]{\left[#1\right]}
\newcommand{\ccompl}[1]{{#1}^*}
\newcommand{\contr}[1]{[#1]}
\newcommand{\harm}[2]{{#1}\,\#\,{#2}} %{{#1}\,\oplus\,{#2}}
\newcommand{\hharm}{\#} %{\oplus}
\newcommand{\rec}[1]{1/#1}
\newcommand{\rrec}[1]{{#1}^{-1}}
\DeclareRobustCommand{\bigO}{%
\text{\usefont{OMS}{cmsy}{m}{n}O}}
\newcommand{\dalyba}{/}%{\oslash}
\newcommand{\mmax}{\mbox{\tiny $\max$}}
\newcommand{\thr}[2]{\mathrm{Th}^{#1}_{#2}}
\newcommand{\rectbound}{h}
\newcommand{\pol}[3]{\sum_{#1\in #2}{#3}_{#1}\prod_{i=1}^n x_i^{#1_i}}
\newcommand{\tpol}[2]{\min_{#1\in #2}\left\{\skal{#1,x}+\const{#1}\right\}}
\newcommand{\comp}{\circ} % composition
\newcommand{\0}{\vec{0}}
\newcommand{\drops}[1]{\tau(#1)}
\newcommand{\HY}[2]{F^{#2}_{#1}}
\newcommand{\hy}[1]{f_{#1}}
\newcommand{\hh}{h}
\newcommand{\hymin}[1]{f_{#1}^{\mathrm{min}}}
\newcommand{\hymax}[1]{f_{#1}^{\mathrm{max}}}
\newcommand{\ebound}[2]{\partial_{#2}(#1)}
\newcommand{\Lpure}{L_{\mathrm{pure}}}
\newcommand{\Vpure}{V_{\mathrm{pure}}}
\newcommand{\Lred}{L_1} %L_{\mathrm{red}}}
\newcommand{\Lblue}{L_0} %{L_{\mathrm{blue}}}
\newcommand{\epr}[1]{z_{#1}}
\newcommand{\wCut}[1]{w(#1)}
\newcommand{\cut}[2]{w_{#2}(#1)}
\newcommand{\Length}[1]{l(#1)}
\newcommand{\Sup}[1]{\mathrm{Sup}(#1)}
\newcommand{\ddist}[1]{d_{#1}}
\newcommand{\sym}[2]{S_{#1,#2}}
\newcommand{\minsum}[2]{\mathrm{MinS}^{#1}_{#2}}
\newcommand{\maxsum}[2]{\mathrm{MaxS}^{#1}_{#2}} % top k-of-n function
\newcommand{\cirsel}[2]{\Phi^{#1}_{#2}} % its circuit
\newcommand{\sel}[2]{\sym{#1}{#2}} % symmetric pol.
\newcommand{\cf}[1]{{#1}^{o}}
\newcommand{\Item}[1]{\item[\mbox{\rm (#1)}]} % item in roman
\newcommand{\bbar}[1]{\underline{#1}}
\newcommand{\Narrow}[1]{\mathrm{Narrow}(#1)}
\newcommand{\Wide}[1]{\mathrm{Wide}(#1)}
\newcommand{\eepsil}{\varepsilon}
\newcommand{\amir}{\varphi}
\newcommand{\mon}[1]{\mathrm{mon}(#1)}
\newcommand{\mmon}{\alpha}
\newcommand{\gmon}{\alpha}
\newcommand{\hmon}{\beta}
\newcommand{\nnor}[1]{\|#1\|}
\newcommand{\inorm}[1]{\left\|#1\right\|_{\mbox{\tiny $\infty$}}}
\newcommand{\mstbound}{\gamma}
\newcommand{\coset}[1]{\textup{co-}{#1}}
\newcommand{\spol}[1]{\mathrm{ST}_{#1}}
\newcommand{\cayley}[1]{\mathrm{C}_{#1}}
\newcommand{\SQUARE}[1]{\mathrm{SQ}_{#1}}
\newcommand{\STCONN}[1]{\mathrm{STCON}_{#1}}
\newcommand{\STPATH}[1]{\mathrm{PATH}_{#1}}
\newcommand{\SSSP}[1]{\mathrm{SSSP}(#1)}
\newcommand{\APSP}[1]{\mathrm{APSP}(#1)}
\newcommand{\MP}[1]{\mathrm{MP}_{#1}}
\newcommand{\CONN}[1]{\mathrm{CONN}_{#1}}
\newcommand{\PERM}[1]{\mathrm{PER}_{#1}}
\newcommand{\mst}[2]{\tau_{#1}(#2)}
\newcommand{\MST}[1]{\mathrm{MST}_{#1}}
\newcommand{\MIS}{\mathrm{MIS}}
\newcommand{\dtree}{\mathrm{DST}}
\newcommand{\DST}[1]{\dtree_{#1}}
\newcommand{\CLIQUE}[2]{\mathrm{CL}_{#1,#2}}
\newcommand{\ISOL}[1]{\mathrm{ISOL}_{#1}}
\newcommand{\POL}[1]{\mathrm{POL}_{#1}}
\newcommand{\ST}[1]{\ptree_{#1}}
\newcommand{\Per}[1]{\mathrm{per}_{#1}}
\newcommand{\PM}{\mathrm{PM}}
\newcommand{\error}{\epsilon}
\newcommand{\PI}[1]{A_{#1}}
\newcommand{\Low}[1]{A_{#1}}
\newcommand{\node}[1]{v_{#1}}
\newcommand{\BF}[2]{W_{#2}[#1]} % Bellman-Ford
\newcommand{\FW}[3]{W_{#1}[#2,#3]} % Floyd-Washall
\newcommand{\HK}[1]{W[#1]} % Held-Karp
\newcommand{\WW}[1]{W[#1]}
\newcommand{\pWW}[1]{W^{+}[#1]}
\newcommand{\nWW}[1]{W^-[#1]}
\newcommand{\knap}[2]{W_{#2}[#1]}
\newcommand{\Cut}[1]{w(#1)}
\newcommand{\size}[1]{\mathrm{size}(#1)}
\newcommand{\dual}[1]{{#1}^{\ast}}
\def\gcd#1{\mathrm{gcd}(#1)}
\newcommand{\econt}[1]{C_{#1}}
\newcommand{\xecont}[1]{C_{#1}'}
\newcommand{\rUn}[1]{\fontas{L}^{\downarrow}(#1)}
\)
Can the L(A)/Max(A) gap be large?
-
As before, for a finite set $A\subseteq\NN^n$ of vectors, $\Un{A}$ denotes the minimum size of a Minkowski
$(\cup,+)$ circuit producing the set $A$ by starting with $n+1$ single element
sets $\{\vec{0}\},\{\vec{e}_1\},\ldots,\{\vec{e}_n\}$,
and $\MMax{A}$ (resp., $\MMin{A}$) denotes the minimum size of a tropical $(\max,+)$ (resp., $(\min,+)$ circuit) solving the maximization (resp., minimization) problem on the set $A$ (as feasible solutions): given an input weighting $x\in\RR_+^n$, compute the maximum (resp., minimum) of $\sum_{i=1}^na_ix_i$. A set $A\subseteq\NN^n$ is an antichain if
$a,b\in A$ and $a\leq b$ imply $a=b$ (no two vectors of $A$ are comparable under $\leq$).
Theorem 3.6 in the book shows that the gap $\MMax{A}/\MMin{A}$ can be even exponential; in particular, such a gap is achieved on the antichain
$A\subseteq\{0,1\}^{\binom{n}{2}}$ of characteristic $0$-$1$ vectors of (simple) paths from $1$ to $n$ in $K_n$. Thus, since $\MMax{A}\leq \Un{A}$ holds for any set $A\subseteq\NN^n$,
the gap $\Un{A}/\MMin{A}$ can also be exponential.
Problem 1(1) in the book asks whether also the gap
$\MMin{A}/\MMax{A}$ can be super-polynomial for an antichain $A$ (see also
the paragraph below Problem 1 for why only antichains are here interesting). Actually, it is even unknown whether the gap $\Un{A}/\MMax{A}$ can be large.
Problem A:
Can the gap $\Un{A}/\MMax{A}$ be super-polynomial on antichains $A\subseteq\{0,1\}^n$?
Remark: Note that besides being an antichain, the set $A$ is required to consist of only $0$-$1$ vectors. If vectors of $A$
are allowed to have also larger entries, then the gap $\Un{A}/\MMax{A}$ can be even exponential.
Namely, there there are antichains $A\subseteq \NN^n$ such that $\MMax{A}=O(n)$
but $\Un{A}=2^{\Omega(n)}$. This is actually shown in
Remark 1.35(2)
of the book by considering the maximization problem on $A$ instead of the minimization problem: given an input weighting $x\in\RR^n_+$,
take $x_0:=\max\{x_1,\ldots,x_n\}$ instead of $x_0=\min\{x_1,\ldots,x_n\}$. The separating sets $A\subseteq\NN^n$ are
$d$-homogeneous for $d:=\lceil n/2\rceil$. Note that each such set $A$
lies in the convex hull of the set $B=\{d\cdot\vec{e}_1, d\cdot\vec{e}_2,\ldots,d\cdot\vec{e}_n\}$, the $i$th of which has $d$ in the $i$th position and zeros elsewhere.
$\Box$
Problem A has an equivalent reformulation in terms of Minkowski circuits alone.
For a set $A\subseteq\NN^n$,
$\Down{A}$ denotes (as in the book) the set of all vectors $b\in \NN^n$ such that $b\leq a$ holds for at least one $a\in A$. Let
\[
\rUn{A}:=\min\{\Un{B}\colon A\subseteq B\subseteq\Down{A}\}
\]
be the minimal size of a Minkowski $(\cup,+)$ circuit producing a set $B$ satisfying $A\subseteq B\subseteq\Down{A}$.
By Lemma 1.31(3), we know that for every antichain $A\subseteq\{0,1\}^n$ the equality $\MMax{A}=\rUn{A}$ holds. So, Problem A is equivalent to
Problem A':
Can the gap $\Un{A}/\rUn{A}$ be super-polynomial on antichains $A\subseteq\{0,1\}^n$?
Footnotes:
 Jump back ☝
Jump back ☝
 Jump back ☝
Jump back ☝
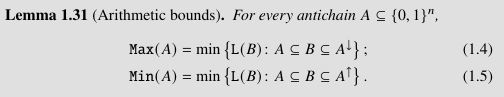 Jump back ☝
Jump back ☝
⇦ Back to the comments page
 Jump back ☝
Jump back ☝
 Jump back ☝
Jump back ☝
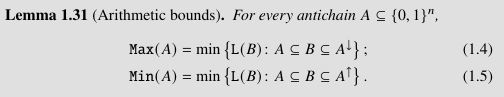 Jump back ☝
Jump back ☝