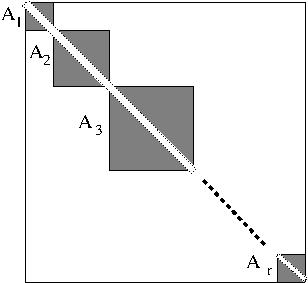
Theorem (Sergeev [3]): \[ \OR_2(K)=\Omega(n\log n). \]Proof: Recall that rows and columns of $K$ are labeled by subsets of $[r]=\{1,\ldots,r\}$, where $n=2^r$ is the dimension of $K$. For $0\leq i\leq r$, let $A_i$ the $m_i\times m_i$ sumbatrix of $K$ with $m_i=\tbinom{r}{i}$, whose rows are labeled by subsets of size $i$, and columns by subsets of size $r-i$. Note that the submatrices $A_i$ do not share common rows or columns. This implies $\OR_2(K)\geq \sum_{i=0}^r\OR_2(A_i)$.

On the other hand, each of the submatrices $A_i$ has $0$s on the diagonal, and $1$s elsewhere. That is, each $A_i$ is just the complement $\overline{I}_{m_i}$ of the identity $m_i\times m_i$ matrix $I_{m_i}$. The matrix $\overline{I_m}$ is the adjacency matrix of the complete (non-bipartite) graph $\mathrm{K}_m$ on $m$ vertices. Well-known results of Hansel and Krichevski (see here) imply that every covering of $\mathrm{K}_m$ by bicliques (bipartite complete subgraphs) must have weight $m\log m$; the weight of a biclique is the number of its vertices, and the weight of a covering is the sum of weights of its bicliques. When translated to the language of OR-circuits, this implies that $\OR_2(A_i)\geq m_i\log m_i$ for all $i=1,\ldots,r-1$. Thus, \[ \OR_2(K)\geq \sum_{i=1}^{r-1}m_i\log m_i=\sum_{i=1}^{r-1}\binom{r}{i}\log \binom{r}{i} \geq \sum_{i=1}^{r-1}\binom{r}{i}\log \Big(\frac{r}{i}\Big)^i = \sum_{i=1}^{r-1}\binom{r}{i} i \log \frac{r}{i} =\Omega(r2^r)=\Omega(n\log n). \] $\Box$