Let us shortly recall some notation used in the book [3]. A boolean $n\times n$ matrix $R$ is a rectangle if it consists of some $a\times b$ all-$1$ submatrix, and has $0$s elsewhere. The weight of such a rectangle is $w(R):=a+b$. A covering (or a $\SUM$-covering) of a boolean $n\times n$ matrix $A$ is a collection $\f = \{ R_1, \ldots, R_k \}$ of $n\times n$ rectangles such that $A=R_1+R_2+\cdots+R_k$. The weight of such a covering $\f$ is $w(\f):= w(R_1)+\ldots + w(R_k)$. In these terms, $\SUM_2(A)$ is the minimum weight of a covering of $A$. In the case of $\XOR$-coverings, we consider the sums $A=R_1\oplus R_2\oplus\cdots\oplus R_k$ modulo $2$. In the case of $\OR$-coverings, we consider the componentwise ORs $A=R_1\lor R_2\lor\cdots\lor R_k$. It is clear that every $\SUM$-covering is also an $\OR$- and $\XOR$-covering but not vice versa. In what follows, the measure $\LL$ stands for any of the measures $\SUM$, $\OR$ and $\XOR$. As in the book [3], index "2" in $\LL_2$ stands for "depth-2 circuit complexity", that is, for the $\LL$-covering complexity.
The boolean $n \times n$ Kneser-Sierpinski (or disjointness) matrix $D_n$ is defined for $n=2^r$ as follows. Rows and columns of $D_n$ are labeled by distinct subsets $u \subseteq [r]$, and $D[u,v] = 1$ iff $u \cap v = \emptyset$. It is equivalent to the recursive definition \begin{equation}\label{D} D_1 = \begin{bmatrix} 1 \end{bmatrix}, \qquad D_2 = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}, \qquad D_{2n} = \begin{bmatrix} D_n & D_n \\ D_n & 0 \end{bmatrix}. \end{equation} Kneser-Sierpinski matrices are widely believed candidates to have substantially nonlinear $\XOR_2$-complexity $n^{1+\Theta(1)}$. Unfortunately, so far, we are not able to prove higher than $n\ln^2 n$ lower bound for any explicit $n \times n$ matrix.
For the $\SUM_2$-complexity of $D_n$, the following bounds were shown in [3]: \begin{equation}\label{up} n^{1.16} \prec \SUM_2(D_n) \prec n^{1.28}. \end{equation} Here, the lower bound holds for $\OR_2$-complexity as well, and is probably tight in this model, as argued by Chistikov et al. in [2]. The upper bound is obtained in [3] by constructing coverings based on the recursive definition \eqref{D}.
Recently, Alman, Guan and Padaki [1] obtained a very nontrivial generalization of that method leading to efficient coverings for Kronecker powers of matrices. Recall that the Kronecker product (or a tensor product) of an $n\times m$ matrix $A=(a_{i,j})$ and a $p\times q$ matrix $B$ is an $np\times mq$ matrix of the form \[ A\otimes B=\begin{bmatrix} a_{1,1}B & \ldots & a_{1,m} B\\ \vdots & \ddots & \vdots\\ a_{n,1} B & \ldots & a_{n,m} B \end{bmatrix}\,. \] obtained from matrix $A$ by replacing each its entry $a_{i,j}$ by the matrix $a_{i,j} B$. In the boolean case, the 1-entries of $A$ are replaced by copies of matrix $B$, and 0-entries by all-zero matrices of the size of $B$. The $r$-th Kronecker power $A^{\otimes r}$ of $A$ is the Kronecker product of $r$ copies of $A$, that is, $A^{\otimes r} = A \otimes A \otimes \ldots \otimes A$.
Note that for $n=2^r$, the $n \times n$ Kneser-Sierpinski matrix $D_n$ is the $r$-th Kronecker power of $D_2 = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}$, that is, $D_n = D^{\otimes r}_2$.
The key concept in the method of [1] is the spectral weight of coverings. If $R$ is a rectangle whose all-$1$ submatrix is an $a\times b$ matrix, then the spectral weight of $R$ is defined as $\sigma(R) := \sqrt{ab}$. Analogously, the spectral weight of a covering $\f = \{ R_1, \ldots, R_k \}$ is $\sigma(\f) = \sigma(R_1) + \ldots + \sigma(R_k)$. Further, we can define the spectral $\LL$-complexity $\sigma_{\LL}(A)$ of a matrix $A$ as the minimal spectral weight of its $\LL$-covering.
Note, that the spectral weight is always smaller than the usual weight, since $\sqrt{ab} < a+b$. What is more important, is that the spectral weight respects Kronecker product. Let $\f$ and $\h$ be coverings of matrices $A$ and $B$, that is $A = \sum_{R\in \f} R$ and $B = \sum_{R' \in \h} R'$. Because of the distributivity, \[ (A_1 + A_2)\otimes(B_1 + B_2) = A_1 \otimes B_1 + A_1 \otimes B_2 + A_2 \otimes B_1 + A_2 \otimes B_2\,, \] the collection of rectangles $\f\otimes \h := \{ R \otimes R' \mid R \in F, \, R' \in \h \}$ is a covering of the matrix $A \otimes B$ It immediately follows that $\sigma(\f \otimes \h) =\sigma(\f)\sigma(\h)$. Hence, we have a lower bound \[ \LL_2(A^{\otimes r}) \ge \sigma_{\LL}(A^{\otimes r}) \ge \sigma_{\LL}(A)^r\,. \] A natural question is: can we reverse this inequality in at least some weaker sense. In other words, can we obtain upper bounds similar to \begin{equation}\label{eq:desired} \LL_2(A^{\otimes r}) \le \sigma_{\LL}(A)^{r+o(r)} \end{equation} or at least $\LL_2(A^{\otimes r}) \le \sigma(\f)^{r+o(r)}$ for some $\LL$-coverings $\f$ of a matrix $A$?
Of course, there are some "pathological" cases where this is not possible. Consider, for example, the matrix $A = \begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix}$. Its $r$-th Kronecker power $B=A^{\otimes r}$ is an $n\times n$ matrix for $n=2^r$ with just one (the first) all-$1$ row, that is, an $a\times b$ rectangle with $a=1$ and $b=n$. Hence, $\LL_2(A^{\otimes r})=a+b = 1+2^r$, while $\sigma_{\LL}(A^{\otimes r}) = \sqrt{ab}=\sqrt{n}= 2^{r/2}$.
A general obstacle for the desired upper bounds \eqref{eq:desired} in terms of the spectral weight is the growing narrowness of the covering rectangles. The larger ratio between the sides of a rectangle, the larger ratio between the spectral and the usual weights.
Nevertheless, under some conditions, the authors of [1] were able to overcome the indicated obstacle and to derive the desired bounds. The first situation is when the covering $\f$ satisfies some asymmetry criteria, the second one is when the matrix $A$ is symmetric, and the covering $\f$ is one-sided (this means that all rectangles are stretched in the same direction).
Shortly after, Sergeev [4] proposed an alternative analysis and a more elementary proof for a version of this method in the case of symmetric matrices and basic coverings $\f$ satisfying comparatively weaker conditions.
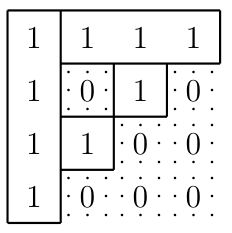
The above methods combine recursive application of spectral-weight-efficient coverings $\f=\{ R_1, \ldots, R_k \}$, transposed coverings $\f^T=\{ R_1^T, \ldots, R_k^T \}$ (in the symmetric case), and some trivial row or column coverings to correct overstretched rectangles. Finally, it occurs that the bound \begin{equation}\label{new} \LL_2(A^{\otimes r}) \preceq \sigma(\f)^r \end{equation} is achievable on some specific coverings $\f$ of matrices $A$. The upper bound \eqref{up} turns out a particular case of \eqref{new}: \[ \SUM_2(D_n) \preceq \sigma_{\SUM}(D_2)^r = \left(\sqrt2 + 1\right)^r \prec n^{1.28}\,, \] if we consider a trivial (and spectral-weight-optimal) covering of $D_2$ by $1 \times 1$ and $1 \times 2$ (or $2 \times 1$) rectangles. The simplest way to improve it is to consider the matrix $D_4$, and its optimal covering depicted on Fig. 1.

In this case, where both methods of [1,4] are applicable, it holds that \[ \SUM_2(D_n) \preceq \sigma_{\SUM}(D_4)^{r/2} = \left(4+\sqrt3\right)^{r/2} \prec n^{1.26}\,. \]
Following the example in Fig. 1, one can consider generalized coverings of larger matrices $D_m$ by width-1 rectangles as a base for constructing. The method of [1] can deal also with $D_8$ case, and the method of [4] with sizes up to $m=2^{15}$. In the latter case, the complexity bound is $\SUM_2(D_n) \prec n^{1.251}$.
An interesting question remains: can we build substantially more efficient $\XOR$-coverings for the Kneser-Sierpinski matrices?
December 21, 2022