Balanced covering of the triangular matrix

For a covering $\sigma$ of a given matrix by rectangles (all-1 submatrices), let $s(\sigma)$ denote the sum of the lengths of shorter sides, and $S(\sigma)$ the sum of the lengths of longer sides of rectangles in $\sigma$. Let $T_n$ be the lower triangular $n\times n$ matrix. Note that $\OR_2(\overline{I_n})\leq 2\cdot \OR_2(T_n)$.

Lemma (Sergeev): For every positive integer $k\leq n$, the matrix $T_n$ has a covering $\sigma$ such that $s(\sigma)=O(n\log n/\log k)$ and $S(\sigma)\leq k\cdot s(\sigma)$.

Note that the trivial covering by rows or by columns on gives $\sigma$ with $s(\sigma)=n$ but $S(\sigma)=\Omega(n^2)$.

Proof: To avoid floorings and ceilings, let us assume that $k$ divides $n$. Call a $p\times q$ rectangle $k$-balanced if $\max\{p,q\}\leq k\cdot \min\{p,q\}$. Let $s'(n)=\min s(\sigma)$, where the minimum is over all coverings $\sigma$ of $T_n$ by $k$-balanced rectangles. Since for such a covering $\sigma$ we have $S(\sigma)\leq k\cdot s(\sigma)$, it is enough to show that $s'(n)\leq 2n\log n/\log k$ for $n\geq k$. We do this by induction on $n$.

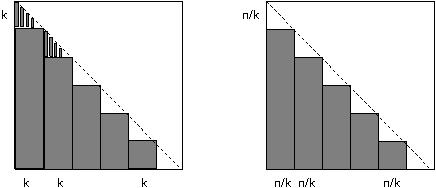
For the induction basis, assume that $n\leq k^2$. In this case we take $n/k$ vertical stripes of width $k$ each, and cover the remaining ones by stripes of width $1$ (see left figure). The resulting covering is $k$-balanced, and we obtain $s'(n)\leq k\cdot(n/k)+n=2n\leq 2n\log n/\log k$.

For the induction step, take $k$ vertical stripes of width $n/k$ each (right figure). The covering is $k$-balanced, since the height of such a rectangle is at most $n-n/k < n= k\cdot (n/k)$. This gives the recurrence $s'(n)\leq k(n/k)+ k\cdot s'(n/k)$. Using the induction hypothesis $s'(m)\leq 2m\log m/\log k$, this yields \[ s'(n)\leq n +k\cdot 2(n/k)\log(n/k)/\log k =n + 2n\log n/\log k - 2n \leq 2n\log n/\log k. \] $\Box$

By taking $k=\sqrt{n}$, we obtain

Corollary: The matrix $\overline{I}_n$ has a covering $\sigma$ such that $s(\sigma)=O(n)$ and $S(\sigma)=O(n^{3/2})$.

S.J. May 2013