Recall that in the $n\times n$ disjointness matrix $D_r$ for $n=2^r$, rows and columns correspond to subsets $u\subseteq [r]=\{1,\ldots,r\}$, and $D_r[u,v]=1$ iff $u\cap v=\emptyset$. We know that $OR_2(D_r)\geq n^{\log_23- 0.5} \geq n^{1.08}$. We also have the following upper bound, even for SUM-circuits.
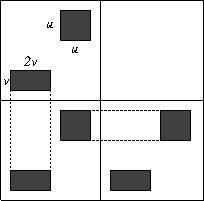
Lemma (Sergeev): There is a constant $c$ such that \[ SUM_2(D_r)\leq c n^{\log_2(1+\sqrt{2})} \approx n^{1.28}. \]Proof: We use the recursive definition of the disjointness $2^r\times 2^r$ matrices $D_r$, $r=1,2,\dots$ \[ D_{r+1}=\left( \begin{array}{cc} D_{r} & 0 \\ D_{r} & D_{r} \\ \end{array} \right) \ \ \mbox{with}\ \ D_1=\left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \\ \end{array} \right) \] The desired decomposition of $D_r$ will consist of "squares" (all-1 submatrices with equal side lengths) and "rectangles" whose side lengths are in relation $1:2$. To decompose the matrix $D_{r+1}$, we use the decompositions of its three submatrices $D_r$, as shown above. In every triple of rectangles, we merge two of them along their longer side (see Figure).

In this way, a $u\times u$ square from the decomposition of $D_r$ generates one square of the same dimension, and one $u\times 2u$ rectangle in the decomposition of $D_{r+1}$. One $v\times 2v$ rectangle generates one rectangle of the same dimensions, and a $2v\times 2v$ square. Thus, if we let $u_r$ be the sum of lengths of the sides of squares, and $v_r$ the sum of lengths of the shorter sides of the rectangles in the decomposition of $D_r$, then we obtain the recursion \[ \begin{bmatrix} u_r \\ v_r \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} u_{k-1} \\ v_{r-1} \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 1 & 1 \end{bmatrix}^k \cdot \begin{bmatrix} u_0 \\ v_0 \end{bmatrix} \] The eigenvalues of the matrix $A= \begin{bmatrix} 1 & 2 \\ 1 & 1 \end{bmatrix}$ are $1\pm \sqrt{2}$. Thus, \[ \begin{bmatrix} u_r \\ v_r \end{bmatrix} = P\cdot \begin{bmatrix} 1+\sqrt{2} & 0 \\ 0 & 1-\sqrt{2} \end{bmatrix}^r \cdot P^{-1} \] for an invertable $2\times 2$ matrix $P$. Thus, both $u_r$ and $v_r$ are at most a constant times $(1+\sqrt{2})^r$, as desired. $\Box$
Reference: